Um bloco de de massa está sob a ação de várias forças e se movimenta ao longo do eixo . A componente da sua velocidade varia com o tempo conforme o gráfico abaixo. Qual é o valor máximo da força resultando sobre o bloco, entre o inicio de seu movimento e ? 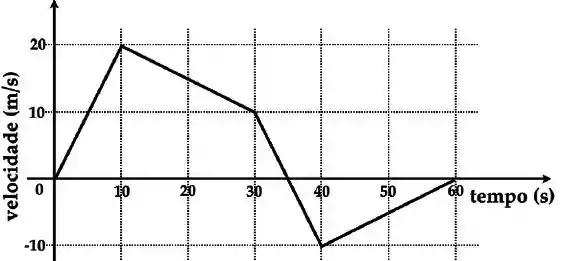
Passo 1
Sabemos que podemos escrever a força usando a segunda lei de Newton, certo?
Assim, precisamos descobrir no gráfico onde temos a maior aceleração em módulo, o que significa a mesma coisa que descobrir onde o gráfico está mais inclinado, já que a aceleração é a inclinação do gráfico da velocidade.
Passo 2
Entre e a inclinação do gráfico é mais acentuada. Assim é só calcular a inclinação para sabermos a aceleração.
Como só estamos interessados no módulo, vamos ficar só com o valor da aceleração, ok?
Passo 3
Agora que já sabemos a massa e a aceleração, conseguimos calcular a força!!