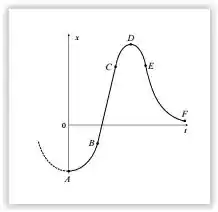
O gráfico abaixo apresenta a evolução temporal da posição x(t) de um objeto em movimento unidimensional. Considerando as informações fornecidas através deste gráfico, assinale dentre as afirmações apresentadas abaixo aquelas que são INCORRETAS.

1. No ponto A temos v = 0.
2. Entre os pontos B e C, representado no gráfico por uma reta, o movimento do objeto é uniforme.
3. No ponto D o objeto está parado e em equilíbrio.
4. Entre os pontos A e B o produto escalar da velocidade e a aceleração satisfaz à condição .
5. A partir do ponto E e até o ponto F o objeto é freado.

1. apenas a (III)
2. apenas as (I), (II) e (V)
3. apenas as (III) e (V)
4. apenas as (I) e (IV)
5. apenas as (II), (III) e (V)
6. não há afirmativas incorretas

Vamos analisar cada uma das afirmativas:

1. No ponto A temos v = 0. Podemos ver que a tangente do gráfico da posição pelo tempo no ponto A é zero. Logo, como essa tangente equivale a velocidade, a velocidade nesse ponto é zero. Verdadeiro
2. Entre os pontos B e C, representado no gráfico por uma reta, o movimento do objeto é uniforme.

No trecho B a C, a tangente se mantem constante, logo a velocidade se mantém constante, já que a tangente de cada ponto desse gráfico equivale a velocidade. Verdadeiro

3. No ponto D o objeto está parado e em equilíbrio.

A velocidade do objeto é zero pelo mesmo motivo do item (i). Mas, como ele tem aceleração, já que no instante seguinte o módulo ta velocidade ta crescendo (tangente), não podemos dizer que ele está em equilíbrio. Podemos pensar pela fórmula , se tem aceleração, tem força resultante, logo não está em equilíbrio. Falso

4. Entre os pontos A e B o produto escalar da velocidade e a aceleração satisfaz à condição .

Vamos lembrar da definição, o módulo do produto escalar é dado por , sendo o ângulo formado pelos dois vetores. Como o movimento é unidimensional, temos duas opções de :

para o caso em que aceleração e velocidade estão em sentidos contrários

para o caso em que aceleração e velocidade estão no mesmo sentido

Vamos analisar:

Velocidade: A velocidade é positiva, já que nesse trecho, a tangente é sempre positiva

Aceleração: Perceba que a velocidade ta aumentando, já que a tangente tá aumentando. Então, a aceleração é positiva também.

Logo, velocidade e aceleração estão no mesmo sentido e o produto escalar é positivo. Verdadeiro

5. A partir do ponto E até o ponto F o objeto é freado.

No ponto E a posição diminui com o tempo e isso indica que a velocidade é negativa.

Por outro lado, a concavidade da curva é positiva, isso indica que a aceleração é positiva.

Assim como a aceleração tem sentido oposto da velocidade o objeto está sendo freiado.

Verdadeiro