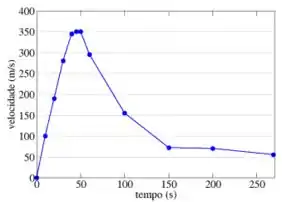
A velocidade de um avião foi medida durante seu percurso, e está graficada abaixo. Estime qual a distância percorrida neste intervalo de tempo.
Passo 1
Bom galera, temos um gráfico da velocidade versus o tempo.
Queremos saber o espaço percorrido.
Como faremos isso?
Bom, lembra que a velocidade é a derivada do espaço? Então, em contrapartida, o espaço é a integral da função velocidade.
Assim:
Show?
Mas nós vamos calcular mesmo essa integral usando funções, métodos de integração, etc?
Não, o que representa a integral nesse gráfico?
Isso ai, a área sob a curva da função!!!!!
Então, vamos tentar calcular a área sob a curva, aproximadamente. Podemos usar figura conhecidas pra isso, achando uma área bem feiamente aproximada, o importante é saber aproximar mais ou menos pois, como você pode ver, as medidas tem ordens de grandeza diferentes ali.
Vamos lá.
Passo 2
Bom, podemos aproximar a área do gráfico assim:
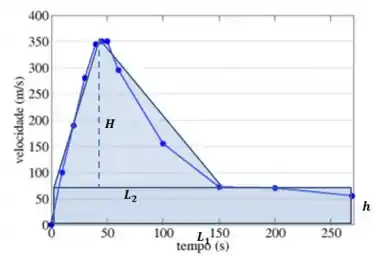
Ta vendo? Coloque ali um triangulo de altura e base e um retângulo de altura e base
Show?
Bom, então vamos calcular a área como:
Onde:
Pra estimar , basta a gente olhar ali o retângulo acaba entre o número e 100. Mesmo raciocínio pra chegar ao numero
Beleza? Então:
Olhando as opções, a que mais se aproxima é:
Faz sentido, afinal, se você olhar o desenho, a gente pegou uma área um pouquinho maior. Então:
a)
Resposta
a)