Cinemática Bidimensional
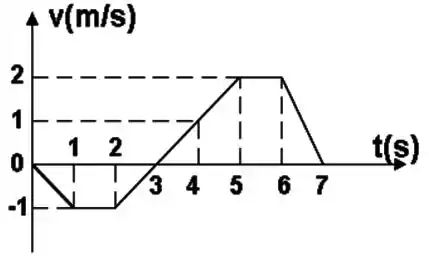
Calcule o deslocamento entre os tempos e de um objeto que se move ao longo de uma linha reta com a velocidade dada pelo gráfico abaixo:
a)
b)
c)
d)
e)
Passo 1
Como nós temos um gráfico de velocidade pelo tempo, temos que a área do gráfico é igual ao deslocamento. Nesse caso, entre os instantes e , temos a área de dois triângulos, onde o triangulo menor corresponde a um deslocamento em direção a origem do movimento, visto que a velocidade é negativa, e o segundo triângulo um deslocamento se afastando da origem, visto que a velocidade é positiva.
Área do triângulo menor:
Área do triângulo maior:
Logo, o deslocamento será:
Visto que os deslocamentos se dão em sentidos contrários. Logo:
Resposta
Alternativa.
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b