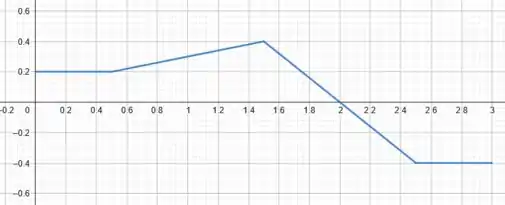
Um motorista entra em uma rua reta, sem saída, com uma velocidade de Ao se deparar com o fim da rua, para, dá marcha a ré e retorna. O gráfico da figura mostra sua aceleração em função do tempo.

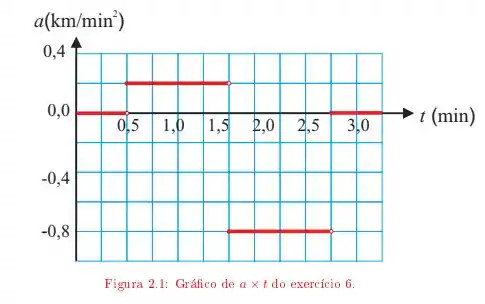
a) Faça o gráfico da velocidade para

Bom, começando pela fase , como a aceleração é nula, a velocidade é constante. Assim:

Show de bola!

Já na fase , temos uma aceleração positiva. Logo:

onde e .

Precisamos deixar tudo na mesma unidade, vamos para .

Se um carro percorre em , quanto ele irá percorrer em ?

É uma regrinha de , se liga só:

Logo:

Perfeito! Então, podemos escrever a velocidade nessa segunda fase pela expressão:

Pois a aceleração só começa em .

Além disso, ao término da fase , teremos:

Excelente!

Indo agora para a fase , como temos aceleração não-nula, a velocidade também será do tipo:

Mas, agora, a nossa “velocidade inicial” será a velocidade final da segunda fase. Assim:

Já a aceleração, pelo gráfico, vale:

Daí:

Pois a fase inicia em .

E, a velocidade final da fase vale:

Ou seja, o carro termina a fase já em movimento de ré.

Por fim, na fase , o carro possui aceleração nula. Ou seja, velocidade constante.

Daí:

Muito bom!

Resumindo tudo que calculamos sobre a velocidade, temos:

Perfeito! Usando essas informações podemos esboçar um gráfico pra velocidade, que será como uma função definida por partes. Nas fases e teremos retas constantes, nas fases e retas inclinadas.

Teremos:

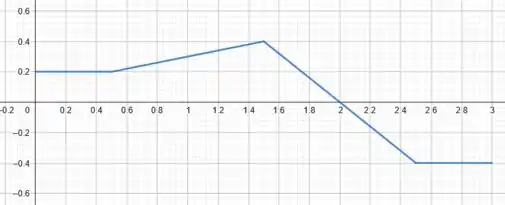
Prontinho galera! Matamos a questão 😊

Até a próxima!