UFRJ – Física 1 – P1 – 2019.2 – Questão 4
Os movimentos de um carro e de um caminhão ao longo de uma estrada em linha reta estão representados nos gráficos de velocidade versus tempo. Os dois veículos estão emparelhados no instante .
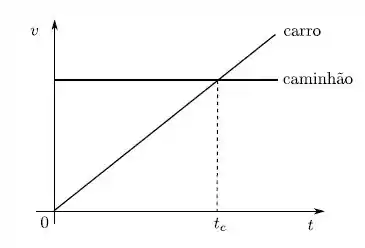
Em um instante posterior , indique a sentença verdadeira sobre estes dois veículos.
- O deslocamento do caminhão é maior do que o do carro.
- O deslocamento do carro é maior do que o do caminhão.
- O caminhão e o carro apresentam o mesmo deslocamento.
- O carro está ultrapassando o caminhão no instante .
- Nenhuma das sentenças acima é correta.
Passo 1
Vamos lá! No item (a) ele diz que o deslocamento do caminhão é maior que o do carro. Vamos verificar?Lembra que a distância percorrida em um gráfico é dada pela área situada entre a curva da velocidade e o eixo do tempo?!
Então
Portanto,
Ou seja, já vimos que as alternativas (b), (c) e (d) são falsas e a alternativa (a) é verdadeira. Como (a) está correta, podemos eliminar também a alternativa (e).
Resposta
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b