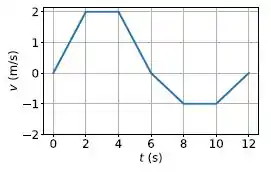
Uma partícula parte da origem em e realiza um movimento retilíneo ao longo do eixo . O gráfico da velocidade da partícula em função do tempo é mostrado na figura abaixo. Assinale o item que fornece o deslocamento no intervalo .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
A questão nos dá o gráfico da velocidade em função do tempo.
Bom, a velocidade nada mais é do que a variação da posição pelo tempo, ou seja, o deslocamento .
Então, queremos calcular esse deslocamento no intervalo de .
Passo 2
Para achar esse deslocamento a partir do gráfico, é só a gente calcular a área debaixo da curva.
Lembrando que quando a velocidade for negativa, devemos colocar sua área também negativa, pois seu deslocamento será na direção contrária. Porém, nesse intervalo de isso não acontece.
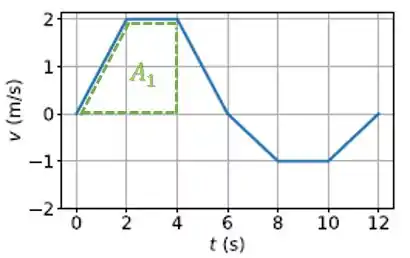
Então, o deslocamento vai ser:
Podemos calcular a área desses trapézios com:
Onde,
- base maior
- base menor
- altura
Com isso, a área será:
OBS: Repara que a unidade será uma unidade de deslocamento , pois ela representa o delocamento na primeira parte do grafico.
Assim achamos o deslocamento de :
Ficamos com a letra (g).
Resposta
Letra (g)