UFABC – Fundamentos de Mecânica – Lista 2 – Questão 5
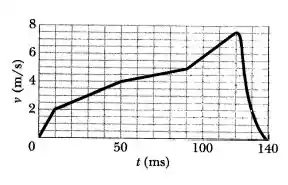
Em um soco para frente no golpe de caratê, o punho, que está em repouso na cintura, é movido rapidamente para frente até o braço ficar completamente estendido. A velocidade v(t) do punho é representada pela Figura abaixo. Determine a distância percorrida pelo punho desde o início do golpe até
(a) o instante t = 50 ms e
(b) o instante em que a velocidade do punho é máxima?
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou te ajudar aqui! O problema deu um gráfico de velocidade versus tempo. E nos perguntou a distância percorrida! Bom, em um gráfico de a área representa numericamente a distância percorrida! Assim, a primeira coisa que temos que ver é a escala do gráfico. Cada quadradinho de unidade de tempo equivale a:
E cada quadradinho de unidade de velocidade equivale a:
Beleza?
Passo 2
Letra (a):
Podemos então separar a primeira região em duas partes: a região de até é um triângulo e a região de até é um trapézio. No desenho fica assim:
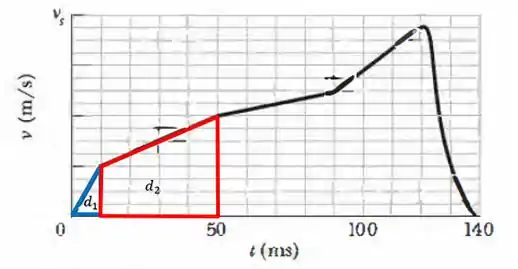
Logo as áreas serão dadas por:
Então a distância percorrida pelo punho do início do golpe até é dada como:
Tranquilo até aqui?
Passo 3
Belezoca, agora na lera (b) queremos a distância até o instante em que a velocidade do punho é máxima, que ocorre no instante .
Já sabemos a distância até , então bora calcular as outras regiões.
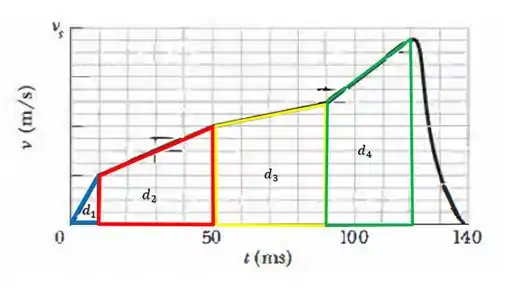
A região de até também é um trapézio, de maneira que:
A região de até também é um trapézio, logo:
Sendo assim, a distância total percorrida será:
E é isso! Espero ter ajudado!