A Figura 3 mostra a aceleração de um ciclista que parte do repouso no instante . O valor máximo da aceleração é .
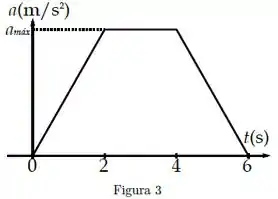
Qual a velocidade do ciclista no instante ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Nessa questão, a gente tem um gráfico da aceleração do ciclista ao longo do tempo e queremos a velocidade final do ciclista.
O que acontece se multiplicarmos a aceleração por um intervalo de tempo?
Vamos ter a variação da velocidade, né.
Então, em cada valor de aceleração em um intervalozinho de tempo, nós temos que a variação da velocidade vai ser dada por .
Ou seja, fazendo isso para todos os pontos, vamos ter que a variação da velocidade é igual à área abaixo do gráfico.
Passo 2
Se o ciclista parte do repouso, sua velocidade final vai ser apenas a variação da velocidade gerada pela aceleração.
Então, vamos achar isso calculando a área abaixo do gráfico.
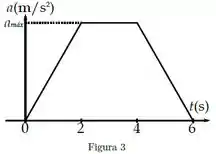
Temos que o gráfico forma um trapézio. Sua área vai ser dada por:
Onde e são as bases maior e menor do trapézio, e sua altura que vai ser .
Substituindo:
Achamos, então, a velocidade do ciclista em e podemos marcar a alternativa (g).
Resposta
Letra (g)