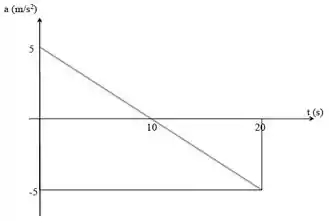
Um corpo é submetido a uma aceleração variável , conforme o gráfico abaixo. No intervalo de a , o instante no qual a velocidade é máxima e a variação total de velocidade no intervalo são, respectivamente:

(a) ; .

(b) ; .

(c) ; .

(d) ; .

(e) ; .

Sobre o instante de ...

Dá uma olhada de novo aqui no gráfico:

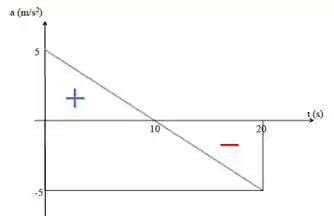
A aceleração é positiva até , então ele ganha velocidade durante esse tempo. Já depois de , a aceleração é negativa, então ele perde velocidade.

Assim, se sua velocidade vai aumentando até , e depois passa a diminuir, esse vai ser o instante de velocidade máxima.

Agora, vamos achar a variação de velocidade.

A sacada aqui é que a área abaixo do gráfico de aceleração pelo tempo nos dá exatamente a variação da velocidade.

Isso porque a variação da velocidade é a integral da aceleração:

E uma integral, nos dá a área abaixo do gráfico.

Então, a variação de velocidade vai ser a soma dessas áreas aqui:

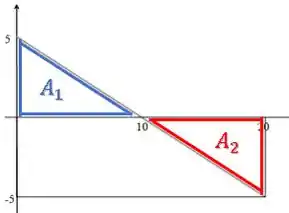
MAS PRESTA ATENÇÃO!!!

Quando a aceleração for negativa, vamos considerar uma “área negativa”. Isso porque uma aceleração negativa gera uma variação de velocidade negativa.

Assim, a variação de velocidade vai ser:

Mas, olha essa simetria dessa reta. De até ela está acima do eixo, enquanto de até ela está abaixo do eixo.

Então, as áreas e são iguais, né?

Assim:

A resposta correta é a alternativa (a).