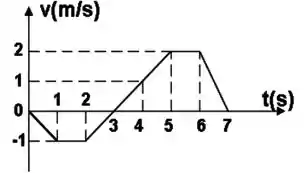
Qual é o módulo e o sentido do deslocamento e da aceleração de um objeto entre os instantes e supondo que o objeto se move ao longo de uma linha reta com velocidade dada pelo gráfico abaixo:
- d = 7,5m e no sentido positivo da reta.
- d = 1,0m e no sentido negativo da reta
- d = 1,5m no sentido positivo e no sentido negativo da reta.
- d = 1,5m e no sentido positivo da reta.
- Nenhuma destas
Passo 1
Bom galeraa, a gente pode calcular tudo isso a partir do gráfico.
Bom, como a velocidade é derivada do deslocamento, a integral da velocidade é igual ao deslocamento:
Bom, mas o que é a integral nesse gráfico ai? Bem, é a área sob o gráfico.
Passo 2
Então:
Essa área pode ser dividida em duas áreas:
A área 1 é a área do triangulo que se forma entre o tempo e . Ela é negativa, já que está abaixo do gráfico:
E a área 2 é a área do triangulo que se forma entre e Assim:
Então:
Então:
Passo 3
Bom, como a aceleração é a derivada da velocidade, e como a derivada de velocidade é o coeficiente da reta tangente à curva da velocidade, podemos calcular a aceleração com a variação da velocidade entre dois tempos:
Passo 4
E o sentido do deslocamento? Bom, como o sinal do deslocamento foi positivo, ele está se deslocando no sentido positivo do eixo
Então:
d)
Resposta
d)