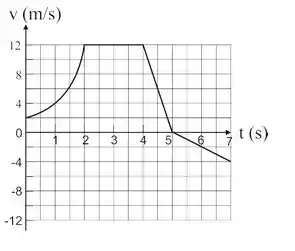
O gráfico ao lado mostra a velocidade de um carro em função do tempo para o intervalo . A expressão da velocidade instantânea, no intervalo de tempo é:
Considerando que o carro em encontra-se na posição , podemos afirmar que sua posição em é:
Dado:
Passo 1
O que ele tá querendo é a posição da partícula em t=7s.
Temos a velocidade da partícula em cada instante de tempo, e com isso podemos encontrar a posição dela. Pra isso vamos usar a seguinte relação :
Então, bora lá resolver:
A primeira parte o enunciado fala pra gente
Resolvendo isso:
Esse foi o deslocamento da partícula entre os instantes e . mas lembra que o enunciado falou que a posição inicial é . Então, a posição da partícula em t=2 s é na verdade a posição inicial mais o quanto ela andou:
Passo 2
Show! Vamos pra outra parte do gráfico. Entre os instantes 2 e 4 temos um segmento de reta horizontal, ou seja, a velocidade é constante, então:
Resolvendo isso:
Então a posição em t=4 s é a posição que ela tava mais o quanto ela andou.\
Passo 3
Vamos pra outra parte do gráfico. Entre os instantes 4 e 5 temos um segmento de reta decrescente. Vamos achar a equação da velocidade em função do tempo para esse segmento.
Temos que , ou seja, a tangente dessa reta. E é o ponto que corta o eixo y. olhando para o gráfico, temos:
Agora, vamos escolher o ponto (5,0) que pertence a reta e substituir na equação, :
Então
Logo:
Resolvendo isso:
Então a posição em t=5 s é a posição que ela tava mais o quanto ela andou.\
Passo 4
Vamos ver agora a última parte do gráfico. Entre os instantes 5 e 7 temos um segmento de reta decrescente. Vamos achar a equação da velocidade em função do tempo para esse segmento.
Temos que , ou seja, a tangente dessa reta. E é o ponto que corta o eixo y. olhando para o gráfico, temos:
Agora, vamos escolher o ponto (5,0) que pertence a reta e substituir na equação, :
Então
Logo:
Resolvendo isso:
Então a posição em t=7 s é a posição que ela tava mais o quanto ela andou.
Maravilha!! Essa é a resposta!
Resposta
37 m