Um objeto de , inicialmente em repouso na origem, é submetido à força variável com o tempo mostrada na figura abaixo.
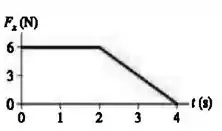
a) Qual a velocidade do objeto em ?
b) Qual a sua posição em ?
Passo 1
a)
Para resolver essa questão, vamos usar a segunda lei de Newton:
A partir disso, podemos passar esse gráfico de vs para vs , conforme abaixo:
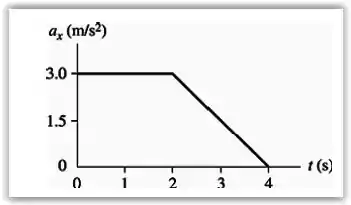
Repare que a força máxima no gráfico do enunciado era 6N. Pela segunda lei de newton:
Isso é justamente o que apresentamos no gráfico.
Passo 2
Beleza! Mas como vamos interpretar esse gráfico? A aceleração não é constante, então fica complicado aplicar as equações da cinemática.
Bom, podemos usar a área do gráfico.
Como , teremos que será dado pela área do gráfico até 4s.
Passo 3
A principio a gente podia pensar em usar a equação de Torricelli, mas não estamos em um movimento uniformemente variado ☹
Não tem jeito! Temos que escrever a equação horária desse movimento! Olhando o gráfico temos que a aceleração é dada por
Passo 4
Integrando essa equação em relação ao tempo
Lembrando que não somei constante na primeira parte para que a nossa velocidade no tempo seja nula como o enunciado fala! Também não somei na segunda parte porque essas duas partes têm que ser iguais para , já que a velocidade é contínua!
Se você quiser calcular nesse caso vai ver que
Como a gente tinha calculado antes!
Passo 5
Agora temos que integrar de novo
De novo temos que usar as condições que e que a posição tem que ser contínua, ou seja, essas duas equações têm que dar o mesmo valor em
Agora basta calcular
Resposta
a)
b)