Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Gráficos do Movimento Retilíneo

Ver Teoria
Exercício 201234567891011121314151617181921222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596

Enunciado

Cinemática Unidimensional

O gráfico abaixo mostra a aceleração e função do tempo de um objeto que se move ao longo de uma linha reta partindo do repouso em t = 0 . Com exceção do instante inicial t = 0 , quando a velocidade do objeto é igual a zero?

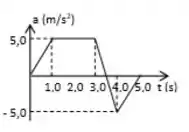
  1. Durante o intervalo de 1,0 a 3,0 segundos.
  2. Em t = 3,5 s .
  3. Em t = 4,0 s .
  4. Em t = 5,0 s .
  5. Em nenhum instante anterior a 5,0 s .

Passo 1

Vamos pegar a equação da velocidade antes de qualquer coisa:

V = V 0 + a t

Como o enunciado diz que V 0 = 0 , temos que

V = a t

Sendo assim, para acharmos a velocidade em qualquer instante, basta calcularmos a área do gráfico.

Mas esta questão vai além. Até t = 3,5 s a velocidade está aumentando ( a > 0 ) , entre t = 3,5 s e t = 5,0 s , a velocidade está diminuindo ( a < 0 ) .

Passo 2

Fazendo a soma das áreas do gráfico para cada intervalo, temos que a área entre t = 0 s e t = 3,5 s é a área do trapézio que pode ser calculada por:

A 1 = 3 , 5 + 2 . 5 2 = 13 , 7 5   m / s

Já a área entre t = 3,5 s e t = 5,0 s é a área de um triângula, que dá:

A 2 = - 1,5   .   5 2 = - 3,75   m / s  

Logo, a aceleração negativa no período de 1,5 s não foi suficiente para anular a velocidade adiquirida nos primeiros 3,5 s . Com isso, dentro destes 5 s não houve ocorrência de velocidade nula.

Resposta

Letra e)

Exercícios de Livros Relacionados

Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b