6) Um projétil é lançado a partir do solo com velocidade de módulo fazendo um ângulo de com a horizontal. Seja o módulo da velocidade no instante . Indique o gráfico que melhor representa em função do tempo.
(a)
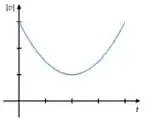
(b)
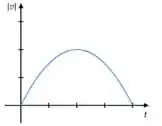
(c)
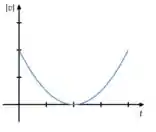
(d)
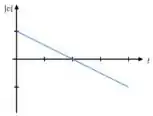
(e)
Passo 1
Fala aí, galerinha!!
Nesse problema a gente tem que encontrar a cara do gráfico do módulo da velocidade em função do tempo. O movimento que o problema nos dá é um lançamento oblíquo então a gente já sabe algumas coisinhas.Nesse tipo de problema é legal a gente reunir todas as informações que a gente sabe sobre a velocidade para saber como que deve ser o comportamento dela. Beleza? Então vamos lá... Como é um lançamento com uma velocidade inicial fazendo um ângulo de com a horizontal, sabemos que o vetor velocidade inicial é dado por:
Beleza... Mas a gente tem que lembrar que em um lançamento horizontal, temos uma aceleração (a aceleração da gravidade ) na direção vertical (), ou seja, a velocidade nessa direção é dada por: e temos um movimento uniforme na direção horizontal . Ou seja, temos um movimento com a velocidade horizontal constante:
É isso que vai nos ajudar a entender o gráfico, beleza? Vamos explorar mais isso aí!
Passo 2
Bom, não podemos esquecer que o gráfico que a gente quer é do módulo da velocidade. Esse módulo é obtido por:
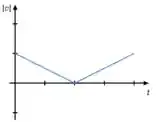
A primeira coisa que a gente pode perceber é que o módulo da velocidade é sempre um número positivo... isso já exclui o gráfico da letra (d) pois ele tem uma parte abaixo do eixo !
A outra coisa é a seguinte, como temos um movimento uniforme na direção , ou seja, é um valor constante diferente de zero, nunca vamos ter pois sempre teremos uma componente com algum valor ali naquela raiz que apareceu. Isso já exclui os gráficos (a), (b) e (c).
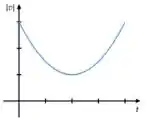
O último fato que a gente pode concluir é que como temos uma aceleração negativa no eixo , temos um movimento neste eixo do tipo lançamento vertical. A gente sabe que a componente começa o movimento com uma velocidade máxima (e aí teremos um valor máximo de ), atinge o valor no ponto mais alto do movimento (valor mais baixo de ) e depois passa a aumentar a velocidade em módulo. O único gráfico que respeita todas essas propriedades desse movimento é:

Resolvemos essa 😊 Vamos para a próxima??
Resposta
(e)