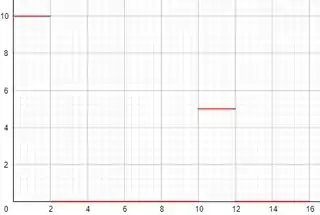
Um carro, numa pista de teste, percorre uma distância reta entre dois pontos com velocidade de acordo com o gráfico abaixo:
Se a escala vertical do gráfico é definida por , determine: (Dê todas as respostas de acordo com o sistema internacional de medidas.)
a distância percorrida pelo carro durante todo o intervalo de tempo;
o gráfico de ;
a velocidade instantânea do carro em e a velocidade média do carro durante todo o percurso. Expresse as respostas com três algarismo significativos e considere que o carro se move na direção ;
a expressão matemática da posição em função do tempo para os intervalos de tempo e . Considere que em a posição do carro é .
Passo 1
Vem comigo que a gente resolve essa juntos!
Para encontrar o tudo que o enunciado pede a gente te que analisar bem esse gráfico. A primeira coisa a fazer é calcular a escala dele.
O ponto máximo na escala vertical é e como no eixo vertical temos quatro divisões, então a cada divisão temos que somar até bater .
Só temos que ficar ligados, que o tempo é contado em segundos e a velocidade em então temos que passar essa velocidade para para isso basta dividir por .
Então vamos analisar e resolver cada item no enunciado nos próximos passos, para não ficar uma coisa muito embolada logo de início.
Vem comigo!
Passo 2
Começando com o item .
Para encontrar a distância percorrida durante os , a gente pode calcular a área do gráfico , já que a área desse tipo de gráfico corresponde a distância percorrida pelo carro.
Vamos dividir o gráfico em figuras geométrias que a gente sabe calcular a área e depois somamos tudo.
Nesse caso teremos um triângulo, dois retângulos e um trapézio. Vamos calcular essas áreas, primeiro a do triângulo no intervalo , temos:
Lembrando que , assim:
Agora a do primeiro retângulo, temos:
Agora a área do trapézio, temos:
Por último a área do segundo retângulo, temos:
Passo 3
Agora que temos todas as áreas, só precisamos somar tudo e termos a distância total percorrida, assim:
Passo 4
Agora vamos para o item .
Agora para determinar o gráfico de , temos que ver o valor da aceleração nos intervalos onde temos variação de velocidade, que no caso é e , e para isso podemos usar a seguinte equação da cinemática, dada por:
O sinal vai depender se a velocidade está aumentando ou diminuindo. Nos instantes que ela é constante quer dizer que a aceleração é zero.
Vamos começar com o intervalo , como a velocidade aumenta, vamos usar o sinal positivo, temos:
Agora para o intervalo , a velocidade diminui nesse intervalo, então vamos usar o sinal negativo, assim:
Passo 5
O gráfico fica da seguinte forma:
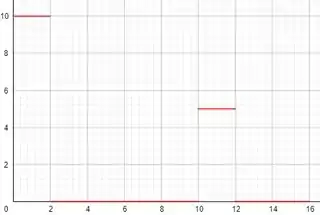
Passo 6
Agora para o item .
Para saber a velocidade instantânea do carro em instante qualquer a única coisa que precisamos fazer é o olhar o valor da velocidade no gráfico no instante que queremos, no caso é em , que pelo gráfico, temos .
Para encontrarmos a velocidade média teremos que dividir a distância total que o carro andou e dividindo pelo tempo do movimento.
No item já calculamos a distância percorrida e encontramos , então temos que a velocidade média é dada por:
Passo 7
Agora vamos para o item .
Temos que montar a equação da posição para dois intervalos de tempo um é com aceleração e o outro com aceleração zero .
A expressão da posição em função do tempo é quando temos aceleração presente é a seguinte:
E quando a aceleração é zero, temo:
Passo 8
Vamos montar essas equações então.
Primeiro para o intervalo com aceleração, segundo o enunciado em temos , logo e pelo gráfico temos , assim:
Agora para o intervalo , nesse caso a posição inicial vai ser o quanto ele andou até esse instante, usando o que calculamos em , temos que e a velocidade é de , assim temos:
Com isso finalizamos essa questão!
Resposta