O gráfico abaixo representa a velocidade de um carro em função do tempo quando ele percorre uma linha reta. O carro inicia o trajeto em primeira marcha. Em , o carro passa da primeira para segunda marcha. Em , o carro passa para terceira marcha. Assinale a afirmativa correta.
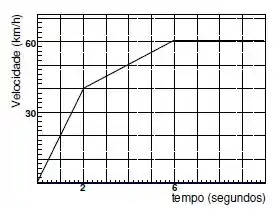
(a) A distância que o carro percorre em segunda marcha é maior que a distância que ele percorre em primeira marcha.
(b) A distância que o carro percorre em segunda marcha é maior que a distância que ele percorre em terceira marcha.
(c) A maior aceleração do carro ocorre quando o carro está em segunda marcha.
(d) A distância que o carro percorre em primeira marcha é maior que a distância que ele percorre em terceira marcha.
(e) A maior aceleração do carro ocorre quando ele está em terceira marcha.
(f) A aceleração quando o carro está em primeira marcha é igual àquela quando ele está em segunda.
Passo 1
Nós temos um gráfico da velocidade do carro pelo tempo. O carro troca de marcha em e .
Então, temos a primeira marcha no intervalo de , a segunda marcha no intervalo de e a terceira marcha no intervalo de .
Além disso, temos que em cada uma das duas primeiras marchas a velocidade varia proporcionalmente com o tempo (reta crescente), portanto teremos dois movimentos uniformemente variados (MUV), já na terceira marcha, a velocidade é constante com relação ao tempo (reta horizontal), logo teremos um movimento uniforme (MU).
Para responder as alternativas, temos que comparar a distância percorrida e a aceleração em cada marcha.
Passo 2
Para calcular a distância percorrida a partir de um gráfico de velocidade pelo tempo, nós podemos calcular a área abaixo desse gráfico.
Então vamos calcular a distância percorrida em cada uma das três machas:
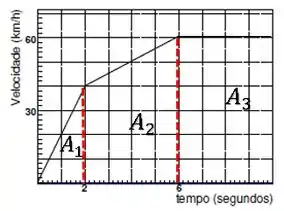
A distância percorrida na marcha 1 () será dada pela área .
A distância percorrida na marcha 2 () será dada pela área .
A distância percorrida na marcha 3 () será dada pela área .
Repare que a velocidade está em e o tempo em . Como vamos apenas comparar as distâncias, não precisamos perder tempo de prova convertendo as unidades. A ideia ainda é a mesma:
Para , vamos calcular a área do triângulo. A base vai de e a altura vai de , pois a cada quadradinho no gráfico, a velocidade sobe .
Para , vamos calcular a área do trapézio. A base pequena vai de , a base grande vai de (0,60) e a altura vai de (2,6):
Para , vamos calcular a área do retângulo. A base vai de (6,10) e a altura vai de (0,60):
Então, descobrimos que:
Logo, a letra (a) está correta , além disso podemos checar que a letra (b) e a letra (d) estão erradas.
Já matamos a questão, mas vamos dar uma olhadinha na aceleração agora.
Passo 3
Em um gráfico da velocidade em função do tempo, podemos calcular a aceleração a partir da inclinação da curva, que nesse caso vão ser três retas. Isso porque a aceleração é dada pela variação da velocidade sobre o tempo:
Então, se pensarmos para um mesmo intervalo de tempo , quanto mais inclinada for a nossa reta, maior será a variação da velocidade para esse intervalo de tempo, e assim, maior é a aceleração.
Com isso, olhando para cada uma das marchas, vemos que na marcha 1, a reta é a mais inclinada de todas (maior aceleração), seguida pela reta na marcha 2 e por último a reta horizontal (aceleração nula) da marcha 3, que representa nenhuma variação de velocidade. Assim, temos que:
As letras (c) ( é máx), (e) ( é máx) e (f) ( estão erradas.
Resposta
Letra (a)