Cinemática Unidimensional
Uma partícula move-se ao longo do eixo com velocidade dada pelo gráfico versus mostrado na figura.
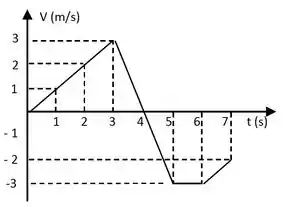
Pede-se:
- O intervalo de tempo onde a intensidade (módulo) da aceleração é máxima;
- O deslocamento nos primeiros seis segundos.
Passo 1
Como a aceleração é a derivada da velocidade, temos que a intensidade da aceleração será máxima quando a derivada da curva for máxia, vemos que isso ocorre entre e .
Para determinar o deslocamento, quando temos um gráfico , basta calcular a área:
Entre e , temos:
Entre e :
Logo, o deslocamento é:
Resposta
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b