A figura abaixo mostra o gráfico da velocidade em função do tempo para uma partícula que se move ao longo da direção horizontal.
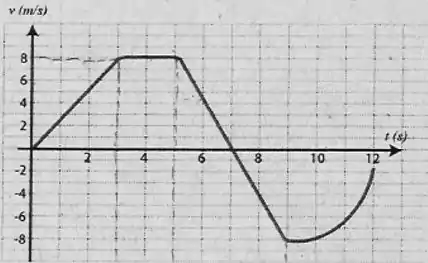
a) Qual é a aceleração da partícula em ?
b) Qual é a distância percorrida pela partícula nos primeiros ?
c) Esboce a curva da aceleração da partícula em função do tempo no gráfico indicado ao lado.
d) Se no intervalo , a equação que descreve a velocidade é dada por , qual é a aceleração da partícula em ?
Passo 1
a)
Basta lembrar que a aceleração é a derivada da velocidade, ou seja, é a inclinação da reta tangente ao gráfico. Isso pode ser calculado imaginando um triângulo no gráfico.
Como a reta é decrescente, então a tangente é, na verdade, negativa. Logo:
Passo 2
b)
Como temos um gráfico de velocidade pelo tempo, a distância percorrida é dada pela área da curva. Logo:
Essa curva pode ser divida em 4 figuras geométricas, calculando a área:
Passo 3
c)
Basta lembrar que a aceleração é a inclinação na reta. Abaixo mostramos o gráfico de velocidade pelo tempo do enunciado e o respectivo gráfico da aceleração pelo tempo.
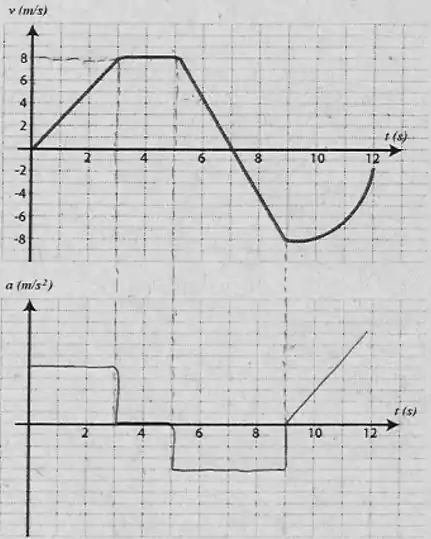
Passo 4
d)
Como já fizemos aqui varias vezes, basta derivar a velocidade para encontrar a aceleração:
Resposta
a)
b)
c)
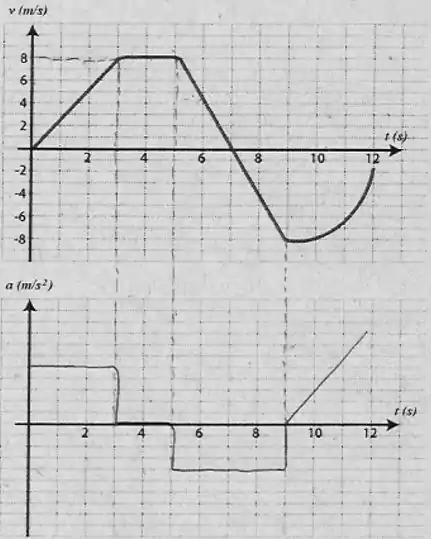
d)