USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 7b
O gráfico da velocidade em função do tempo para uma partícula que sai da origem e se move ao longo do eixo está representado na figura .
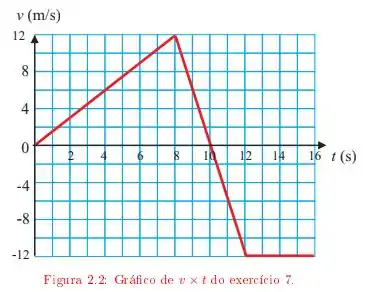
b) Quantos metros a partícula terá percorrido ao todo, para frente e para trás, no fim de segundos? Qual é o valor de neste instante?
Passo 1
E aí gente, tudo beleza?
Nessa questão recebemos o gráfico da velocidade de uma partícula em função do tempo. Através dele, usando as relações cinemáticas:
E:
Bem como as equações características do MRUV e do MRU, chegamos, no item anterior, na seguinte expressão para :
Tranquilo?
Aqui nesse item precisamos determinar a distância total percorrida pela partícula em , bem como a posição que ela se encontra nesse instante.
Então, vamos usar a nossa expressão para bem como o gráfico dado para responder essas perguntas 😊
Vem com a gente!!
Passo 2
Então galera, vamos começar pensando em que momento de a a partícula inverteu o seu movimento...
Analisando o gráfico dado de , isso deve ocorrer quando a sua velocidade se tornou nula. Nesse momento, houve inversão no sentido da velocidade. Pelo gráfico dado:
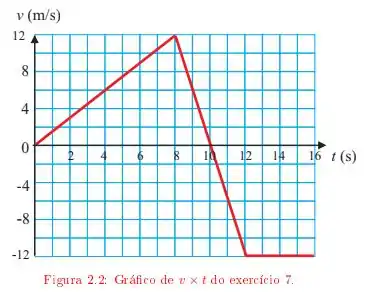
Isso ocorre em .
Tomando , temos:
Portanto, nos primeiros a partícula percorreu . A partir desse instante ela começa a recuar. Em teremos:
Show! Vamos pensar juntos então: se em a partícula estava em , e em , ela está em , quanto que ela recuou nesse período?
Portanto, a distância total percorrida pela partícula em segundos, será dada pela soma do tanto que ela andou pra frente com o tanto que ela andou pra trás. Ou seja:
E, como já foi visto, em , ela se encontra em:
Muito bom, galerinha 😊