Um objeto descreve um movimento unidimensional durante um certo intervalo de tempo. A velocidade deste objeto em função do tempo é dada pelo gráfico abaixo. Identifique neste gráfico, respectivamente, os pontos de máxima aceleração e maior distância da origem.
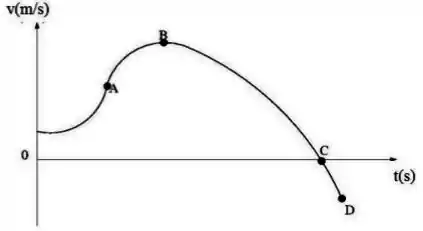
a) pontos e
b) pontos e
c) pontos e
d) pontos e
e) pontos e
Passo 1
Temos um gráfico de velocidade x tempo. Primeiro o problema quer o ponto de máxima aceleração. Basta lembrar que:
Ou seja, a aceleração é a derivada (variação) da velocidade. Para encontrar a maior aceleração é só achar o ponto em que a velocidade teve a maior variação. Graficamente, a variação pode ser representada como uma reta tangente aos pontos do gráfico.
Feito isso, a maior aceleração será aquela que possuir a reta com maior inclinação. Observando o gráfico vemos que a maior inclinação ocorre no ponto .
Passo 2
Agora precisamos saber a maior distância da origem, vamos assumir que a partícula está na origem em . Agora é só pensar analogamente que:
Ou seja, a velocidade é a derivada do espaço. Para isolarmos o espaço, basta fazermos o inverso da derivada, a integral:
Agora é só lembrar que graficamente, a integral nada mais é que a área do gráfico.
O erro mais comum é achar que o ponto é onde o gráfico cobrirá a maior distância. Na verdade, ele cobrirá a maior área. Entretanto, entre o ponto e , o gráfico irá cobrir uma área “negativa”. Pois a velocidade é negativa entre estes pontos. A partícula estará retornando a origem a partir desse ponto. Então o ponto que cobrirá a maior distância é o ponto .
Resposta
Letra (b)