Cinemática Unidimensional
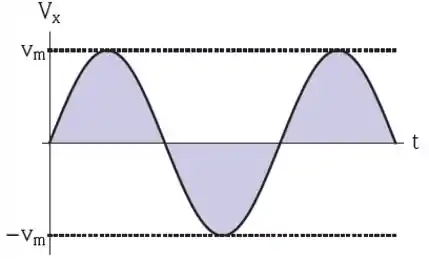
Uma partícula que se move ao longo do eixo está na posição no instante inicial. A figura mostra a velocidade da partícula em função do tempo. As três áreas em cinza que aparecem na figura possuem o mesmo valor . Entre os instantes de tempo mostrados na figura, a posição da partícula é limitada por
(a)
(b)
(c)
(d)
(e)
Passo 1
Quando temos um gráfico velocidade x tempo do movimento unidimensional de uma partícula a área debaixo da curva é o deslocamento da partícula! E as 3 áreas cinza valem .
Passo 2
Ou seja,
- Primeiro a partícula parte de e anda pra frente, chegando em .
- Depois, a velocidade é negativa, isso significa que a partícula anda pra trás, voltando à posição .
- Finalmente, ela anda de novo, parando em .
Portanto, a posição da partícula é limitada por .
Resposta
Alternativa (a)
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b