Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Gráficos do Movimento Retilíneo

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596

Enunciado

Origem do Exercício

Um objeto se move em uma trajetória retilínea, com velocidade v em função do tempo t representada pelo gráfico na figura 1 abaixo.

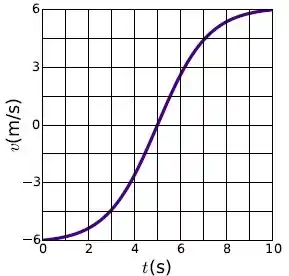
Sejam a 1 a aceleração do objeto em t = 5   s , enquanto a - é a aceleração média entre os instantes 0 e 10   s . Pode-se afirmar que:

  1. a 1 < a - = 1,2   m / s 2
  2. a - = 0,8   m / s 2 < a 1
  3. a 1 = a - = 0
  4. a 1 = a - = 1,2   m / s 2
  5. a - = 1,2   m / s 2 < a 1
  6. a - = 0   m / s 2 < a 1
  7. a 1 = a - = 0,8   m / s 2
  8. a - = 60   m / s 2 < a 1
  9. a 1 < a - = 60   m / s 2

Passo 1

Vamos começar com a aceleração média.

Pra aceleração média, o formato da curva não importa. Ela sempre vai ser:

a - = Δ v Δ t

No nosso caso, a velocidade varia de v = - 6   m / s em t = 0   s até v = 6   m / s em t = 10   s . Assim:

a - = 6 - - 6 10 - 0 = 12 10 = 1,2   m / s 2

Temos uma informação boa: a - = 1,2   m / s 2 .

Ok, mas várias das opções têm a - = 1,2   m / s 2 . Entra em cena o passo 2 !

Passo 2

Vamos avaliar agora a aceleração no tempo t = 5   s . Sabemos que a aceleração instantânea é a tangente do gráfico v × t .

Agora olhe para o nosso gráfico. Ele faz uma curva bem no início, e uma curva mais lá pro fim. E pior ainda, na parte mais “reta” é difícil pegarmos pontos bons para calcular essa tangente.

Como podemos fazer?

Bem, vamos ter que fazer uma aproximação rápida. Note que a parte mais reta passa NA TRAAAAVE dos pontos t = 4   s , v = - 3   m / s e t = 6   s ,   v = 3   m / s . Então vamos aproximar com eles.

tan ⁡ θ = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e ≈ 3 - - 3 6 - 4 = 6 2 = 3   m / s 2

Ou seja:

a 1 ≈ 3   m / s 2

Mas é aproximadamente e não tem nenhum “aproximadamente” nas respostas!

Porém, pelo gráfico, nossa aproximação não deve estar tãaaao errada assim. Então mesmo que não tenhamos 3   m / s 2 , temos algo próximo. De qualquer forma, vai valer que:

a - < a 1

Agora sim! A resposta certa é a letra (e).

e )   a - = 1,2   m / s 2 < a 1

Veja que não tem um valor de a 1 nessa resposta. Então pra afirmamos o que está escrito NÃO precisamos de um valor muito “exato” pra a 1 .

Resposta

Letra (e)

e )   a - = 1,2   m / s 2 < a 1

Exercícios de Livros Relacionados

Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b