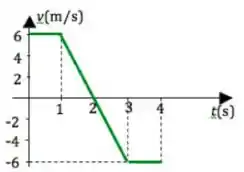
Uma partícula move-se ao longo do eixo . No instante , sua posição é . A figura mostra como varia a velocidade da partícula em função do tempo. A velocidade média entre e é:
a)
b)
c)
d)
e)
Passo 1
Se você não caiu na pegadinha, tá de parabéns! Apesar dele ter pedido a velocidade média até o tempo de , ele deu o gráfico de 4, então não vamos usar ele todo.
Passo 2
Para calcular a velocidade média, precisamos primeiro calcular o deslocamento, que é dado pela área do gráfico:
Entre e a velocidade é positiva e o deslocamento será dado pela área do trapézio de altura , base menor e base maior
Entre e a velocidade é negativa e o deslocamento será dado pela área do triângulo de altura e base multiplicado po
E o deslocamento total será dado por
Passo 3
Sendo assim podemos finalmente calcula a velocidade média
Resposta
a)