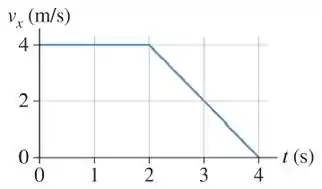
A figura ao lado mostra um gráfico de velocidade por tempo de uma partícula que se move ao longo do eixo . Sua posição inicial é . Em que posição ela estará em ?
(A)
(B)
(C)
(D)
(E)
Passo 1
Temos um gráfico da velocidade em função do tempo.
Com esse gráfico, nos podemos calcular o deslocamento a partir da área abaixo da curva até .
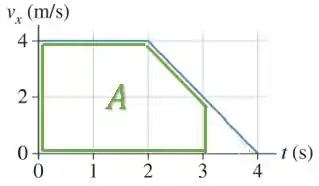
Passo 2
Podemos dividir essa área em duas:
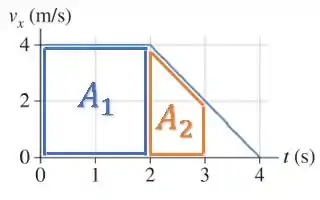
é a área de um retângulo:
é a área de um trapézio:
Logo, o deslocamento é:
Passo 3
Porém, a partícula já se encontrava inicialmente na posição .
Então, sua posição final é:
Ficamos com a alternativa (D).
Resposta
Letra (D)
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b