A figura ao lado representa a trajetória de uma partícula restrita a mover-se em um
plano durante .
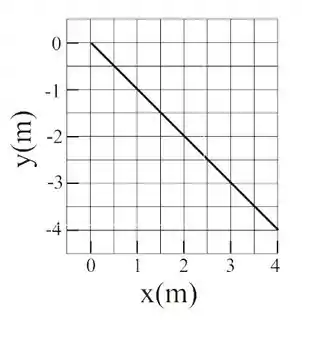
Os símbolos e representam a base de vetores unitários do sistema cartesiano.
O vetor posição que pode ser associado a esta trajetória é:
Passo 1
Considerando que a velocidade inicial é zero, e como sendo um movimento uniformemente variado, temos que, a equação que relaciona a posição com o tempo é:
Além disso, a figura mostra o movimento ao longo de 2 segundos. Então no inicio, ou seja no tempo , vemos que e .
Vamos olhar pra cada coordenada separadamente.
Para t=2 s:
Então
Agora, para x:
Para t=2 s:
Então
Dessa forma temos que:
Resposta
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b