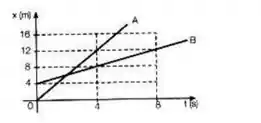
O gráfico representa as funções das posições de duas partículas, A e B, em função do tempo. Analisando o gráfico, podemos afirmar que o instante de encontro entre as partículas, em , vale:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí!!!
Vamos escrever as funções posição para cada um dos corpos.
E depois igualamos para achar o instante de encontro.
Passo 2
Ambos são uma reta, então eles obedecem a equação de uma reta:
Para o corpo A:
Quando e
A equação da reta com esses eixos fica:
Substituindo os pontos:
O outro ponto:
Então para o copro A:
Passo 3
Quando e
A equação da reta com esses eixos fica:
Substituindo os pontos:
O outro ponto:
Então para o copro B:
Beleza?
Passo 4
Eles vão se encontrar quando :
Beleza?
Resposta
Alternativa (b)