Um objeto se move em uma trajetória retilínea, com velocidade em função do tempo representada pelo gráfico na figura 1.
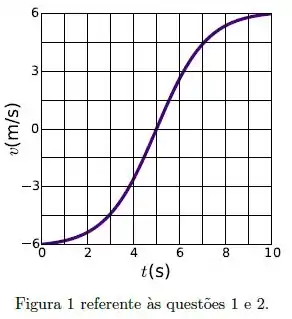
Considere o deslocamento entre os instantes e e o deslocamento entre os instantes e . Assinale a alternativa correta:
Passo 1
O deslocamento entre dois instantes de tempo é a área “embaixo” da curva. Mas muita calma nessa hora.
Quando dizemos que é a área “sob” a curva, queremos dizer em relação ao eixo do tempo . No nosso gráfico, o eixo tá NO MEIO dele! ( corresponde a )
Isso significa que não vamos olhar literalmente a área “embaixo”. Vamos olhar a área formada pelo eixo do tempo e a nossa curva!
Se ela estiver abaixo do eixo, vamos dizer que o deslocamento foi negativo (ou seja, o objeto estava andando pra trás). Se estiver acima, o deslocamento é positivo.
Passo 2
Primeiro vejamos o deslocamento entre e . Isso corresponde à seguinte área:
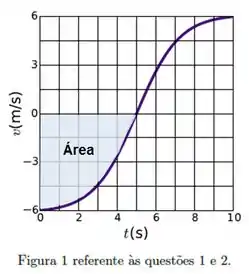
Vamos ter que dar uma aproximada nessa área. Se desenharmos um triângulo aqui...
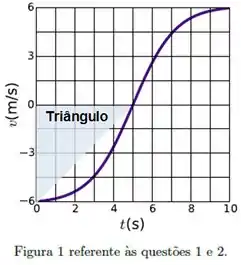
A área do triângulo é um pouco menor que a área entre a curva e o eixo do tempo, mas pelo menos temos alguma coisa:
Temos e . Logo:
O deslocamento corresponde a esse triângulo seria .
A nossa área entre a curva e o eixo do tempo é um pouco maior que a área desse triângulo, digamos que seja . O deslocamento correspondente seria:
Como temos:
Então:
Passo 3
Falta agora . Ele corresponde ao deslocamento dessas duas áreas:
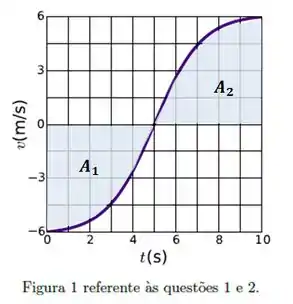
O deslocamento total vai ser a soma dos deslocamentos correspondes a cada uma:
Para aproximar , eu lhe faço um apelo: A figura parece bem simétrica né?
Bem, se considerarmos essas duas áreas aqui aproximadamente iguais...
E aí está! A resposta correspondente é a letra (c).
Resposta
Letra (c)