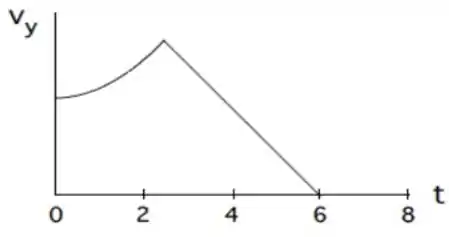
O gráfico abaixo representa a componente vertical da velocidade (em metros/segundo) de um objeto em função do tempo (em segundos). Qual das alternativas melhor descreve o movimento?

a) O objeto acelera para cima com aceleração constante, e depois acelera para baixo até atingir o solo em .

b) O objeto acelera para cima com aceleração constante, e depois acelera para baixo até atingir sua altura máxima em .

c) O objeto acelera para cima com uma aceleração variável, e depois acelera para baixo até atingir o solo em .

d) O objeto acelera para cima com uma aceleração variável, e depois acelera para baixo até atingir sua altura máxima em .

e) Nenhuma das anteriores.

Muito Bem, vamos analisar as alternativas uma a uma.

Alternativa : O objeto acelera para cima com aceleração constante, e depois acelera para baixo até atingir o solo em .

Errado! Lembra que a aceleração é a derivada em relação ao tempo da velocidade? Então, a interpretação geométrica da derivada é a inclinação das retas tangentes às curvas. Confuso? Vou fazer um desenho e você vai entender melhor =)

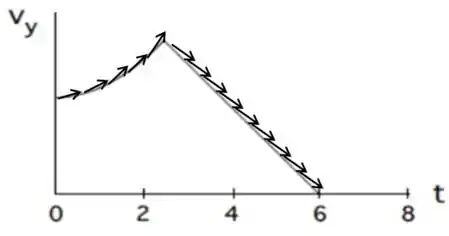
Então, a inclinação dessas retas nada mais é do que a derivada da velocidade naquele ponto, em outras palavras, é a aceleração naquele ponto. Está vendo que as retas mudam de inclinação a todo instante? Isso quer dizer que a aceleração muda de valor a todo instante! Então a aceleração não é constante. Ela é variável.

Além disso, ele diz que no instante , o objeto atingirá o solo, MENTIRA! O objeto tem velocidade positiva durante todo o gráfico. Como ele poderia retornar ao solo? Em nenhum momento o objeto teve uma velocidade negativa que indicaria um movimento de retorno à posição inicial.

O instante indica o ponto em que é nulo. Consegue lembrar qual o momento especial em que se anula? Isso mesmo, a altura máxima, o ponto mais alto que o nosso objeto vai conseguir chegar visto que sua velocidade “acabou”.

Vamos à próxima alternativa!

Alternativa : O objeto acelera para cima com aceleração constante, e depois acelera para baixo até atingir sua altura máxima em .

Errado. Já vimos anteriormente que o objeto não acelera para cima com aceleração constante, e sim com aceleração variável.

Alternativa : O objeto acelera para cima com uma aceleração variável, e depois acelera para baixo até atingir o solo em .

Errado. Já vimos que o instante é o ponto de altura máxima e não de retorno ao solo.

Alternativa : O objeto acelera para cima com uma aceleração variável, e depois acelera para baixo até atingir sua altura máxima em .

Correto!! Finalmente rsrs’. Esta é a opção que perseguiamos. Aceleração variável para cima e altura máxima em .