Cinemática Bidimensional
Determine a aceleração, no movimento dos corpos, pelos gráficos e nos intervalos de tempo determinados:
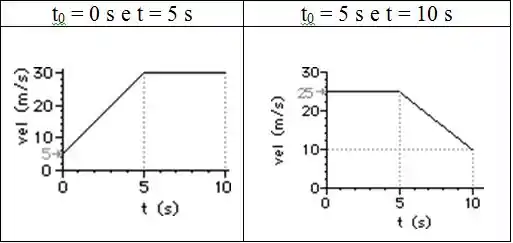
a) ,
b) ,
c) ,
d) ,
e) ,
Passo 1
Basta lembrar que:
Ou seja, a aceleração é a derivada da velocidade. Graficamente, a aceleração é a inclinação da reta da velocidade, ou seja, a tangente do ângulo.
Basta fazer um triangulo retângulo no gráfico e pronto.
No primeiro gráfico temos:
No segundo gráfico temos:
Resposta
Letra (b)
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b