USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 7a
O gráfico da velocidade em função do tempo para uma partícula que sai da origem e se move ao longo do eixo está representado na figura .
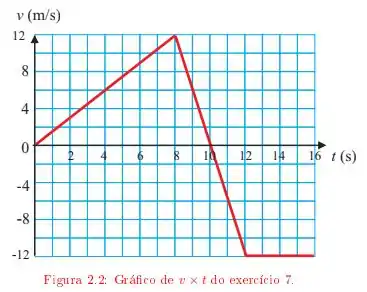
a) Trace os gráficos da aceleração instantânea e da posição para o intervalo de tempo
Passo 1
Fala aí galera, tudo beleza com vocês?
Nessa questão recebemos um gráfico da velocidade de uma partícula em função do tempo e a partir dele precisamos determinar a aceleração, e a posição, e esboçá-las em um gráfico.
Tem duas relações bem importantes envolvendo derivadas e integrais (como você preferir analisar) na cinemática. Vamos revisá-las:
E:
Mas ó, a derivada da velocidade em função do tempo, graficamente é representada pela inclinação da curva em cada ponto. Ou seja, pela tangente à curva em cada ponto.
Já a integral da velocidade em função do tempo é representada graficamente pela área entre a curva e o eixo . Como temos apenas variações uniformes da aceleração, podemos dizer que o espaço será dado por uma equação do grau do tipo:
Sabendo disso, vamos encontrar e pedido na questão 😊
Passo 2
Bom, vamos começar calculando a aceleração em função do tempo.
Como comentamos no passo anterior, ela é dada pela inclinação da curva em cada ponto do gráfico.
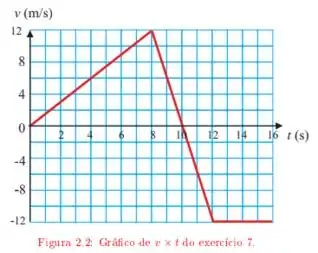
Analisando o gráfico dado vemos que para:
temos uma reta crescente
temos uma reta decrescente
temos uma reta constante
Para cada um desses trechos temos uma inclinação diferente, e portanto, uma aceleração diferente.
No primeiro trecho, a tangente da reta é dada por:
Excelente!
No segundo trecho, teremos:
Portanto:
Já no último trecho, teremos:
Portanto, podemos escrever como sendo:
Plotando esses resultados em um gráfico, temos:
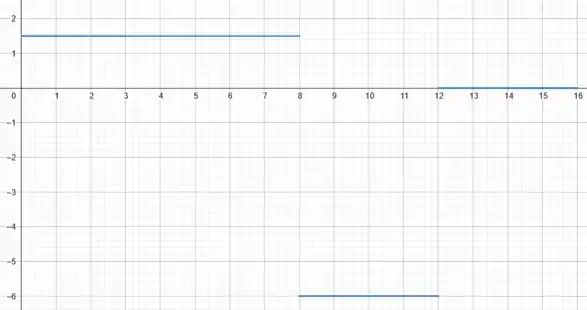
Excelente!
Passo 3
Agora vamos calcular a posição da partícula.
Como comentamos no passo , devemos nos preocupar em calcular a área abaixo da curva.
Novamente, vamos dividir esse estudo nos três trechos do gráfico de .
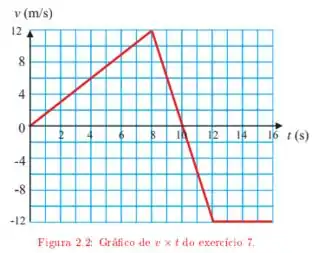
No trecho ,temos uma reta cuja equação é dada por:
Vimos que:
Já , pois a partícula parte do repouso.
Assim:
Se estivermos em um tempo dentro do trecho , a área abaixo da curva é dada por:
Logo:
Quando , temos:
Excelente!
No trecho , até a partícula tem velocidade positiva e move-se para frente. Depois desse instante ela passa a recuar.
Aqui vamos buscar calcular a posição usando a equação:
onde
Para isso, vamos considerar que:
E:
Daí, vamos ter:
Logo:
Por fim, no último trecho, , temos a velocidade constante. Então:
onde:
Temos:
Perfeito! Juntando tudo isso, temos:
A partir disso, podemos esboçar o seguinte gráfico para :
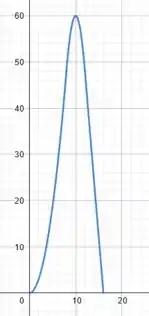
Perfeito pessoal!!
Com isso, encerramos a questão!
Muito obrigado pela atenção de vocês 😉
Resposta
Resposta no texto.