USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 13a
Um objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
a) Faça o gráfico da velocidade em função do tempo para o intervalo de tempo , indicando os instantes em que a velocidade é nula e em que ela é máxima (positiva);
Passo 1
Fala aí pessoal, tudo beleza?
Nessa questão temos um objeto que parte do repouso, ou seja:
E que se desloca com velocidade:
Precisamos traçar um gráfico para essa velocidade em função do tempo para . Além disso, também precisamos calcular os instantes em que a velocidade é nula e em que ela é máxima.
Para identificar esses pontos, basta igualarmos a expressão de , e também identificarmos o ponto de máximo dessa função. Pra essa segunda parte podemos derivar a expressão de e igualar a .
Vamo nessa!
Passo 2
Vamos começar identificando os instantes em que a velocidade é nula.
Temos:
Essa expressão só se anula, se:
Massa!
Para identificar os pontos de velocidade máxima, vamos derivar a expressão dada e igualá-las a .
Temos:
Porta
Nesse pontao, a velocidade deverá ser máxima.
Passo 3
Para esboçar o gráfico correspondente a essa velocidade, vamos analisar a sua expressão:
É a equação de uma parábola virada para baixo. Como já vimos no passo anterior, essa parábola possui raízes em e , e ponto de máximo em .
Logo, temos o seguinte gráfico:
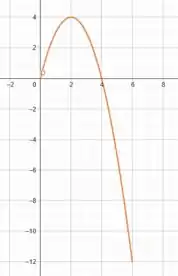
Excelente!
Curtiram a solução? Responde Aí.
Resposta
