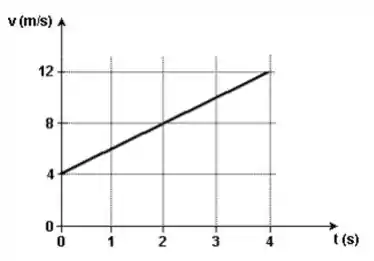
O gráfico da velocidade em função do tempo de um ciclista, que se move ao longo de uma pista retilínea, é mostrado a seguir. Considerando que ele mantém a mesma aceleração entre os instantes t = 0 e t = 7 segundos, determine a aceleração e a distancia percorrida neste intervalo de tempo. Expresse sua resposta no SI
Passo 1
Bom, a questão pelo gráfico nos deu a Velocidade Final, a Velocidade Inicial e o tempo! Com isso já podemos calcular a aceleração né? É só lembrar que
Show!
Passo 2
E agora que a gente tem a aceleração fica MUUUITO fácil de calcular a distância, né? É só usarmos a formulinha do sorvetão! Como a quetão quer em t=7, simbora:
Lindíssimo!
Resposta
e
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b