Em , uma partícula localizada em tem uma velocidade de no sentido de positivo. A aceleração da partícula varia com o tempo como mostrado na figura. Qual é a posição da partícula em ?
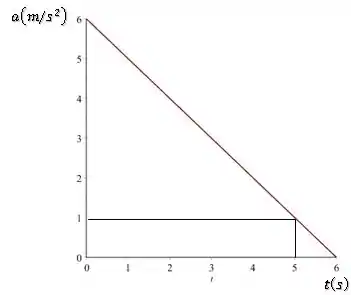
Figura: Aceleração da partícula em função do tempo
A.
B.
C.
D.
E.
Passo 1
Quando a gente tem uma aceleração igual a zero, estamos falando de um Movimento Uniforme.
Quando a gente tem uma aceleração constante, estamos falando de um Movimento Uniformemente Variado.
Mas e quando temos uma aceleração variável???

Bom, esse movimento a gente não sabe as equações para trabalhar, né.
Então, vamos ter que a partir do gráfico da aceleração achar a velocidade e a partir da velocidade achar a posição .
Vamos fazer isso usando a famosa integral.
Se integrarmos , achamos uma variação de velocidade .
E se integrarmos a , achamos uma variação da posição .
Passo 2
Primeiro de tudo vamos achar a função .
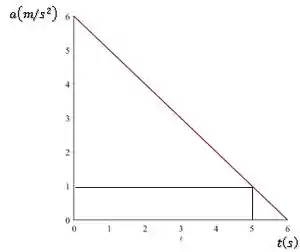
O gráfico é de uma reta, e passa pelos pontos , .
Assim, a equação da reta fica:
Passo 3
Agora que temos a função da aceleração sobre o tempo, podemos integrar num intervalo para encontrar a .
Porém, como queremos uma função e não especificamente a velocidade no instante , vamos integrar num intervalo de até um tempo :
A gente sabe que a velocidade no instante inicial é :
Estamos meio caminho andado!
Passo 4
Agora que temos a função da velocidade, podemos achar a função da posição .
Vamos fazer a mesma coisa que antes.
Primeiro vamos integrar sobre um intervalo de a , para achar a variação da posição . Feito isso, vamos substituir pelo instante :
Sabemos que a posição inicial é :
Prontinho, temos a expressão da posição em função do tempo.
Passo 5
Agora, basta substituir o instante :
Ficamos com a letra D.
Resposta
Letra (D)