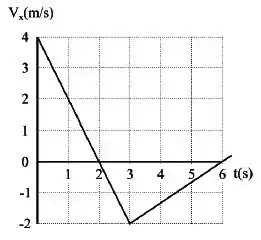
é a velocidade de uma partícula movendo-se ao longo do eixo , conforme mostra o gráfico ao lado. Se em, qual é a posição da partícula em ?
(a)
(b)
(c)
(d)
(e)
Passo 1
Temos o gráfico da velocidade da partícula em função do tempo.
O que conseguimos analisando um gráfico desses?
Conseguimos a variação da posição a partir da área abaixo da curva.

Não entendeu direito? Calma...
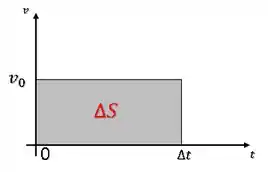
A velocidade é a variação da posição no tempo. Então, se a velocidade for constante, conseguimos o deslocamento simplesmente multiplicando a velocidade pelo intervalo de tempo:
Esse deslocamento nos dá o mesmo valor que essa área abaixo da reta aqui (área do retângulo):
Mas no caso da nossa questão, temos uma velocidade diferente para cada intervalo de tempo.
Porém, a ideia da área abaixo da reta para calcular o deslocamento se matém correta.
É como se a gente pegasse a velocidade em cada intervalozinho de tempo muito pequeno e calculasse esse deslocamento a partir da área abaixo desse retângulozinho . No final, teremos a área toda abaixo da curva/reta e o deslocamento total. (Princípio da querida integral do cálculo).
Passo 2
Vamos aplicar essa idéia.
Se a partícula está na posição em , vamos calcular o deslocamento da partícula entre e e somar à posição inicial.
Para calcular o deslocamento no intervalo , basta calcular essa área aqui:
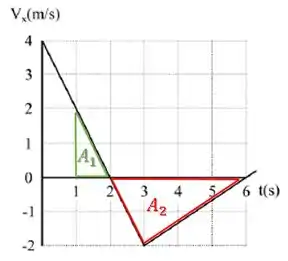
ATENÇÃO!!!
A área abaixo do eixo (em vermelho), entra como negativa, uma vez que uma velocidade negativa contribui para um deslocamento contrário.
Então, o deslocamento total será a soma da área (positiva) com (negativa):
Para achar faremos a área do triângulo:
Para , também calcularemos a área de um triângulo:
Então, o deslocamento será:
Passo 3
Agora que achamos o deslocamento e sabemos a posição inicial , vamos achar a posição da partícula em .
Ficamos com a alternativa (d).
Resposta
Letra (d)