O gráfico a seguir mostra como varia a velocidade de uma partícula, que se move ao longo do eixo , em função do tempo.
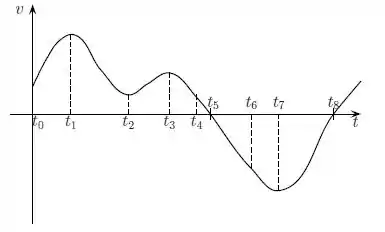
Sabendo que no instante a partícula se encontrava na origem, qual a única correta das afirmativas a seguir?
(a) A aceleração da partícula é nula no instante .
(b) No instante sua aceleração é positiva.
(c) A partícula inverte o sentido do movimento no instante .
(d) No instante a partícula volta à origem.
(e) Entre os instantes e a partícula se move no sentido positivo do eixo .
(f) A aceleração média entre os instantes e é nula.
Passo 1
Inicialmente a partícula se encontra na origem e ela se movimento somente ao longo de uma reta.
Sua velocidade será indicada pela função do gráfico :

Vamos analisar cada uma das alternativas.
Passo 2
(a) A aceleração da partícula é nula no instante .
Novamente...
A aceleração é a variação da velocidade.
A variação de um gráfico é dada pela sua inclinação (derivada).
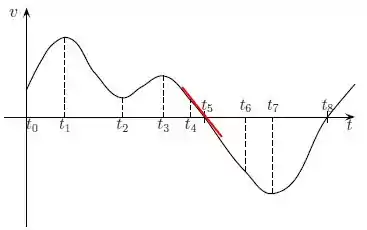
Em , o gráfico apresenta uma inclinação negativa, assim, a aceleração nesse instante é negativa.
A alternativa (a) está incorreta.
Passo 3
(b) No instante sua aceleração é positiva.
A aceleração é a variação da velocidade.
A variação de um gráfico é dada pela sua inclinação (derivada).
A inclinação no instante é negativa (inclinada para baixo):
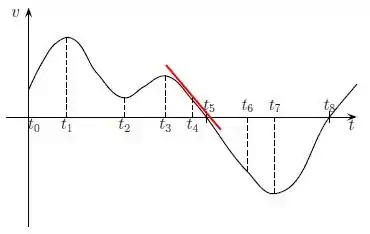
Assim, a aceleração é negativa nesse instante, ou seja, a velocidade está diminuindo.
A alternativa (b) está incorreta.
Passo 4
(c) A partícula inverte o sentido do movimento no instante .
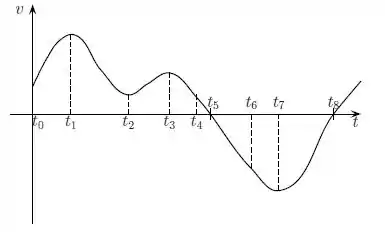
De novo, não podemos confundir o gráfico da posição com o da velocidade .
No instante , o gráfico passa a ser decrescente, porémmmmmm, a velocidade ainda apresenta um valor positivo, ou seja, a partícula ainda anda no sentido positivo do eixo .
A alternativa (c) está incorreta.
Passo 5
(d) No instante a partícula volta à origem.
No instante , o valor de velocidade volta a ser zero, ou seja, a partícula para momentâneamente.
Mas e todo o deslocamento no sentido positivo do eixo que ela teve antes de parar?
Isso mesmo, ela não voltou à origem, apenas parou de avançar.
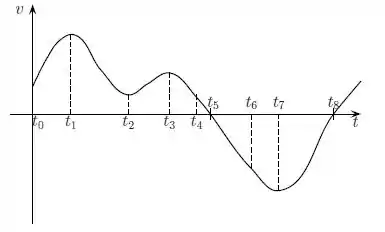
OBS: Lembrando que o deslocamento da partícula nesse gráfico é igual à área abaixo do gráfico.
Assim, a partícula só volta à origem quando a área em Verde (deslocamento no sentido positivo do eixo ) for compensada pela área em Vermelho (deslocamento no sentido negativo do eixo .
A alternativa (d) está incorreta.
Passo 6
(e) Entre os instantes e a partícula se move no sentido positivo do eixo .
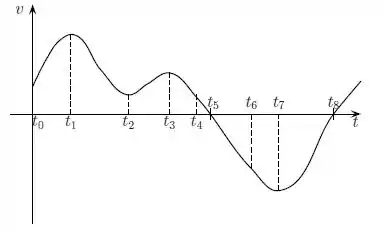
Podemos ver pelo gráfico que entre os instantes e , a velocidade é sempre positiva (gráfico acima do eixo ), por mais que existam trechos crescentes e decrescentes.
Se a velocidade é positiva, a partícula se move na direção positiva do eixo .
A afirmativa (e) está correta.
Não podemos confundir com o gráfico da posição pelo tempo ... nesse caso, se o gráfico tivesse um trecho decrescente, a partícula se moveria no sentido contrário do eixo .
Passo 7
(f) A aceleração média entre os instantes e é nula.
Acabamos de ver que a aceleração é dada pela inclinação do gráfico da velocidade.
Entretanto, a aceleração média entre dois pontos, será a inclinação média entre eles, ou seja, a inclinação da reta que liga esses pontos:
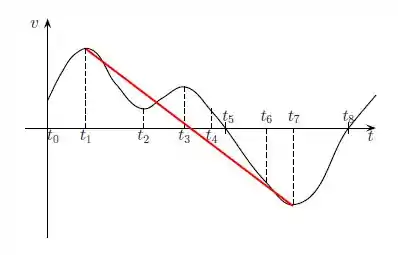
Como a reta é decrescente, a aceleração é negativa entre os instantes e .
A alternativa (f) está incorreta.
Resposta
Letra (e)