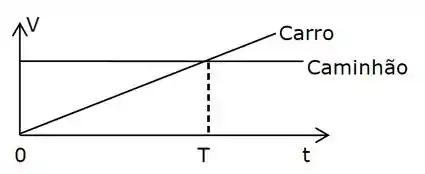
Os movimentos de um carro e um caminhão ao longo de uma estrada reta são representados pelo gráfico de velocidade-tempo abaixo. Os dois veículos estão inicialmente lado a lado no tempo .
No momento T, o que é verdade das distâncias percorridas pelos veículos desde o tempo ?
A) Eles terão viajado a mesma distância.
B) O caminhão não terá se movido.
C) O carro terá viajado mais longe do que o caminhão.
D) O caminhão terá viajado mais longe do que o carro.
E) O carro está acelerando, logo irá mais longe que o caminhão.
Passo 1
Vamos analisar esse gráfico.
Primeira coisa é olhar os eixos, pra ver o que tá sendo medido. Temos um gráfico da velocidade pelo tempo.
Uma relação importante que sempre ajuda é:
Ou seja, a aceleração do movimento é igual a inclinação da reta, ou seja, igual a tangente da reta.
Então se tem uma reta horizontal, como é o caso do caminhão, temos que a velocidade não varia, ou seja a aceleração é zero, e temos um MU.
Quando temos uma reta inclinada, quer dizer que a velocidade varia linearmente com o tempo. Ou seja, a aceleração é constante, portanto temos um MUV.
Agora, é só analisar cada movimento de acordo.
Passo 2
O enunciado fala pra gente que os dois tem a mesma posição inicial, vamos chamar de .
Para o caminhão, temos um MU. A equação que relaciona a posição e o tempo é:
Então a posição do caminhão no instante é:
Beleza!
Vamos ver agora o carro. Temos um MUV, então:
Vamos usar aquela relação que falamos lá em cima:
Calculando a tangente da curva, temos:
Beleza. Substituindo:
Lembrando que a velocidade inicial do carro é zero.
A posição do carro no instante é:
Então, vamos comparar as posições do caminhão e do carro:
Então, o caminhão está mais distante do que o carro. Que corresponde a letra D.
Resposta
Alternativa d.