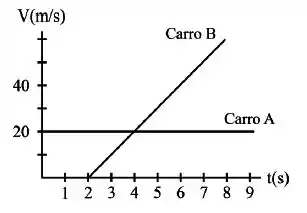
O motorista A está dirigindo ao longo de uma estrada. O motorista B começa a dirigir quando o carro A passa por ele. Os gráficos de suas velocidades são mostrados na figura abaixo. Em que instantes de tempo os carros A e B estarão lado a lado na estrada?
(a) ,
(b) ,
(c) ,
(d) ,
(e) ,
Passo 1
O motorista B começa a dirigir quando o carro A passa por ele. Apesar de um pouco ambígua, essa frase nos diz que quando B começa seu movimento , o carro A está passando por ele.
Então já sabemos que será o primeiro instante onde os carros se encontrarão.
Mas dá uma olhada no gráfico, o carro A realiza um movimento uniforme (reta horizontal) e o carro B realiza um movimento uniformemente variado (reta inclinada). Se a velocidade de B vai aumentando, em algum instante ele vai alcançar o carro A.
Passo 2
Para achar esse segundo instante de encontro devemos olhar para as distâncias percorridas por cada um.
A primeira opção seria construir a equação da posição de cada um desses carros para depois igualá-las. Mas se liga no bizu...
A área abaixo do gráfico de velocidade pelo tempo nos dá exatamente o deslocamento.
Opaa, então vamos olhar a distância que cada um percorre e ver quando eles se encontram.
A partir do momento que os carros estão juntos , o carro A vai percorrer uma distância dada pela área do retângulo até um instante desconhecido .
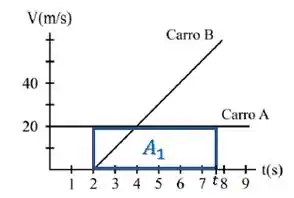
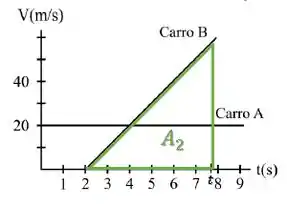
Já o carro B, vai percorrer uma distância dada pela área do triângulo :
Como os carros partem juntos, enquanto a velocidade de A for maior que a de B , eles se afastam.
Essa diferença do quanto o carro A andou a mais que o carro B pode ser calculada pela área entre as retas. Chamaremos essa diferença de :
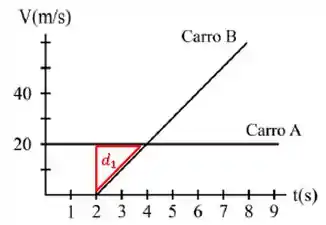
Depois de , o carro B tem velocidade maior e começa a se aproximar do carro A.
Agora, a área entre as retas representa o quanto o carro B anda a mais que o carro A. Chamaremos essa diferença de :
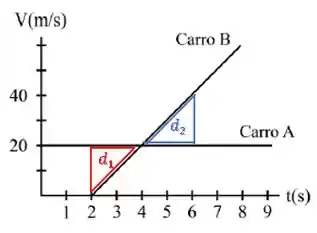
Mas agora vem o bizu. Se queremos que os carros se encontrem, queremos que (o quanto o carro A andou a mais que B entre ) seja igual a (o quanto o carro B anda a mais que o carro A após ). Ou seja:
Para que essas áreas sejam iguais, por simetria podemos dizer que a base do triângulo de área deve ter um comprimento de .
Portanto, eles voltam a se encontrar em .
Assim, temos que os carros estão lado a lado em e . Ficamos com a alternativa (d).
Resposta
Letra (d)