Profº Sato - Listas de Cálculo 1 de Cálculo 1 da UFU - 2ª Lista de Exercícios

Calcule as derivadas sucessivas até a ordem dada

Calcule as derivadas sucessivas até a ordem dada

Enuncie a regra da derivada da função inversa. Use este resultado para calcular a derivada da

função

A quantidade de carga em coulombs (C) que passa através de uma seção reta de um fio até

o instante (medido em segundos) é dada por

Calcule a primeira derivada da função

Encontre em que instante a corrente é mais baixa

A quantidade de carga em coulombs (C) que passa através de uma seção reta de um fio até

o instante (medido em segundos) é dada por

Calcule a primeira derivada da função

Encontre a corrente quando: e

Calcule a primeira derivada da função usando as regras de derivação

Calcule a primeira derivada da função usando as regras de derivação

Calcule a primeira derivada da função usando as regras de derivação

Calcule a primeira derivada da função usando as regras de derivação

Calcule a primeira derivada da função usando as regras de derivação

DEm cada caso, escreva a função dada na forma de uma composta , identificando a função e a função . Em seguida, encontre a derivada da função

Em cada caso, escreva a função dada na forma de uma composta , identificando a função e a função . Em seguida, encontre a derivada da função

Em cada caso, escreva a função dada na forma de uma composta , identificando a função e a função . Em seguida, encontre a derivada da função

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Determine as derivadas das funções

Determine as derivadas das funções

Calcule a primeira derivada da função usando as regras de derivação

Calcule a primeira derivada da função

Calcule a primeira derivada da função

Determine as derivadas das funções

Determine as derivadas das funções

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Usando o teorema da função implícita, encontre da função a seguir

Faça a dedução da derivada da função

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

Encontre a velocidade desse movimento no instante .

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

Quando a velocidade é máxima?

Determine as derivadas das funções

em que é uma constante real e um natural maior do que .

Determine as derivadas das funções

Determine as derivadas das funções

Calcule as derivadas sucessivas até a ordem dada

Calcule as derivadas sucessivas até a ordem dada

Calcule as derivadas sucessivas até a ordem dada

Calcule as derivadas sucessivas até a ordem dada

Em cada caso, escreva a função dada na forma de uma composta , identificando a função e a função . Em seguida, encontre a derivada segunda da função

Em cada caso, escreva a função dada na forma de uma composta , identificando a função e a função . Em seguida, encontre a segunda derivada da função

DEm cada caso, escreva a função dada na forma de uma composta , identificando a função e a função . Em seguida, encontre a segunda derivada da função

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

Encontre a fórmula Fase-Amplitude desse movimento.

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

Faça o desenho dos gráficos da velocidade e posição,

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

Quando a massa passa pela posição de equilíbrio pela primeira vez?

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

A que distância da posição de equilíbrio a massa chega?

Nos itens que seguem, use a Regra de L’Hôspital onde for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique por quê.

Nos itens que seguem, use a Regra de L’Hôspital onde for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique por quê.

Nos itens que seguem, use a Regra de L’Hôspital onde for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique por quê.

Nos itens que seguem, use a Regra de L’Hôspital onde for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique por quê.

Nos itens que seguem, use a Regra de L’Hôspital onde for apropriado. Se existir um método mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique por quê.

Mostre que

para qualquer inteiro positivo n. Isso mostra que a função exponencial tende mais rapidamente ao infinito que qualquer potência de x.

Mostre que

para todo número p > 0. Isso mostra que a função logaritmo tende a infinito mais vagarosamente que qualquer potência de x.

Calcule as derivadas sucessivas das funções

Em seguida, para cada uma delas determine uma lei de formação, ou seja, expresse

Para cada uma das funções , em que e são dadas a seguir, faça o que se pede

(a) e

(a.a) Reescreva f (x), usando uma propriedade dos logaritmos, como

em que e . Em seguida, use a regra da cadeia para obter .

Para cada uma das funções , em que e são dadas a seguir, faça o que se pede

(b) e

(b.a) Reescreva f (x), usando uma propriedade dos logaritmos, como

em que e . Em seguida, use a regra da cadeia para obter .

Para cada uma das funções , em que e são dadas a seguir, faça o que se pede

(c) e

(c.a) Reescreva f (x), usando uma propriedade dos logaritmos, como

em que e . Em seguida, use a regra da cadeia para obter .

A função , aparece em aplicações para a sintetização de frequência modulada (FM).

(a) Use uma calculadora gráfica para esboçar um gráfico da função f (x), em seguida, use esse gráfico para dar um esboço, mesmo que grosseiro, do gráfico de sua derivada f ′ (x).

A função , aparece em aplicações para a sintetização de frequência modulada (FM).

(b) Calcule f′(x) e utilizando uma calculadora gráfica plote seu gráfico. Compare com o obtido no item (a).

Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:

(a)

Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:

(b) f ′ (x) > 0 para x 0;

Trace o gráfico de uma função contínua y = f (x), tendo todas as seguintes propriedades:

(c) f” (x) > 0 para x 0 para x > 0;

Explique o significado das expressões ”indeterminadas”abaixo e exemplifique esta situação:

(a) Produtos Indeterminados

(b) Diferenças Indeterminada

(c) Potências Indeterminadas

Nos itens que seguem, use a Regra de L’Hôspital onde for apropriado. Se existir um método

mais elementar, use-o. Se a Regra de L’Hôspital não for aplicável, explique por quê.

Se um objeto de massa m é solto a partir do repouso, um modelo para sua velocidade v após t

segundos, levando-se em conta a resistência do ar, é

onde g é a aceleração da gravidade e c é uma constante positiva. (a) Calcule

Qual o significado desse limite?

Se um objeto de massa m é solto a partir do repouso, um modelo para sua velocidade v após t

segundos, levando-se em conta a resistência do ar, é

onde g é a aceleração da gravidade e c é uma constante positiva. Para um valor fixo de t, use a Regra de L’Hospital para calcular , o que você pode concluir sobre a velocidade de um objeto caindo no vácuo?

Se um tanque contém, inicialmente, 5.000 galões de água, que escoa pelo fundo em 40 minutos,

então a Lei de Torricelli dá o volume V de água que restou no tanque depois de t minutos como

,em que

Encontre a taxa segundo a qual a água está escoando do tanque depois de: (a) 5 min, (b)

10 min, (c) 20 min e (d) 40 min.

Se um tanque contém, inicialmente, 5.000 galões de água, que escoa pelo fundo em 40 minutos,

então a Lei de Torricelli dá o volume V de água que restou no tanque depois de t minutos como

,em que

Em que instante o fluxo é mais rápido? E mais vagaroso? Resuma o que você encontrou.

Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao

longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza

da força é

onde µ é uma constante chamada coeficiente de atrito. Encontre a taxa de variação de F em relação a .

Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao

longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza

da força é

onde µ é uma constante chamada coeficiente de atrito. Encontre a taxa de variação de F em relação a . Quando essa taxa de variação é igual a 0?

Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao

longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza

da força é

onde µ é uma constante chamada coeficiente de atrito. Se W = 50 lb e = 0, 6, faça um esboço do gráfico de F como uma função de e use-o para localizar o valor de para o qual .

Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a

escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela

escorrega a uma taxa de 5 pés/s.

(b) A que taxa a área do triângulo, formado pela escada, parede e pelo solo, varia?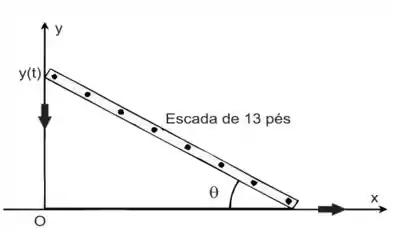

Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a

escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela

escorrega a uma taxa de 5 pés/s.

(c) A que taxa o ângulo, formado pela escada e pelo solo, varia?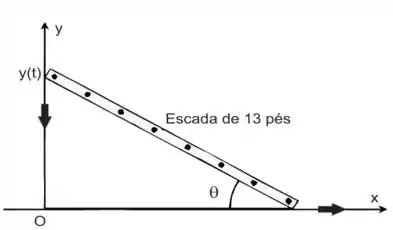

Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa

dada:

Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa

dada:

Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa

dada:

Determinar a equação da reta tangente à curva , que seja paralela à reta . Esboçar os gráficos da função, da reta dada e da reta tangente encontrada. Determine, também, a reta normal à essa curva passando pelo ponto de tangência.

Em qual ponto do gráfico da função a reta tangente é horizontal?

Encontre os pontos sobre a elipse onde a reta tangente tem inclinação 1. Para esses pontos determine, também, a equação da reta normal à curva.

Encontre a reta tangente à astroide + , em que a > 0 é um constante, em um

ponto da curva.

Determine as séries de Taylor das seguintes funções com centro x = 0.

Determine as séries de Taylor das seguintes funções com centro x = 0.

Determine as séries de Taylor das seguintes funções com centro x = 0.

Encontre os valores máximo e mínimo absolutos da função .

Dada a função , obtenha seus pontos de máximo e mínimo relativos e absolutos, sabendo-se que o domínio é D = [0; 6].

Uma empresa foi fundada em 1990 e sua capacidade de produção P = P (t) evoluiu segundo:

1. Em que ano a empresa alcançou sua capacidade máxima de produção?

Uma empresa foi fundada em 1990 e sua capacidade de produção P = P (t) evoluiu segundo:

(b) Qual foi essa capacidade?

Um cartaz deve conter 50 de matéria impressa com duas margens de 4 cm cada, na parte superior e na parte inferior e duas margens laterais de 2 cm cada. Determine as dimensões externas do cartaz de modo que sua área total seja mínima.

Encontre a área do maior retângulo que pode ser inscrito em um semi-cı́rculo de raio r.

Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-

cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso

existam).

Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-

cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso

existam).

Faça um estudo qualitativo das funções dadas a seguir. Em seguida, esboce seus gráfico, desta-

cando os pontos de máximo e mı́nimo locais e/ou globais, pontos de inflexão e assíntotas (caso

existam).

A altura de um objeto que se desloca verticalmente é dada por

,

com h em m e t em segundos. Determine: (a) a velocidade do objeto quando t = 0;

A altura de um objeto que se desloca verticalmente é dada por

,

com h em m e t em segundos. Determine: (b) sua altura máxima e quando esta ocorre;

A altura de um objeto que se desloca verticalmente é dada por

,

com h em m e t em segundos. Determine: (c) sua velocidade quando .

Um objeto de massa m é arrastado ao longo de um plano horizontal sobre a ação de uma força

F agindo ao longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano,

então a intensidade da força é

onde µ, é uma constante chamada coeficiente de atrito. Para qual valor de a F é a menor

possível?

Um barco deixa as docas às 14h e viaja para o sul com velocidade de 20km/h. Outro barco

estava rumando para o leste a 15km/h e alcança a mesma doca às 15h. Em que momento os

dois botes estavam mais próximos um do outro?

Jane está em um barco a 2 km da costa e deseja chegar a uma cidade litorânea localizada 6 km

ao longo de uma linha costeira retilínea desde o ponto (na costa) mais próximo do barco. Ela

rema a 2 km/h e caminha a 5 km/h. Onde ela deve aportar para chegar à cidade no menor

tempo possível?

Uma caixa fechada com base quadrada vai ter um volume de 2000 cm³ . O material da tampa

e da base vai custar R$3, 00 por centímetro quadrado e o material para os lados R$1, 50 por

centímetro quadrado. Encontre as dimensões da caixa de modo que o custo seja mínimo.

Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a

escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela

escorrega a uma taxa de 5 pés/s.

(a) A que taxa o topo da escada escorrega para baixo nesse momento?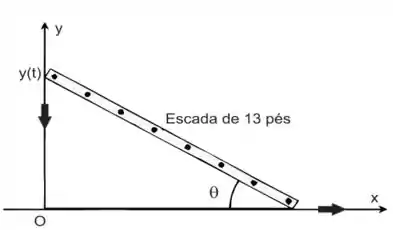

Para cada uma das funções , em que e são dadas a seguir, faça o que se pede

(a) e

(a.b) Aplique o logaritmo na igualdade obtendo

Em seguida, derive essa igualdade, usando o Teorema da função implícita, para obter .

Para cada uma das funções , em que e são dadas a seguir, faça o que se pede

(b) e

(b.b) Aplique o logaritmo na igualdade obtendo

Em seguida, derive essa igualdade, usando o Teorema da função implícita, para obter .

Para cada uma das funções , em que e são dadas a seguir, faça o que se pede

(c) e

(c.b) Aplique o logaritmo na igualdade obtendo

Em seguida, derive essa igualdade, usando o Teorema da função implícita, para obter .

Uma janela tem a forma de um retângulo sob uma semicircunferência. Para um perı́metro de 5

metros, encontre as dimensões de tal janela de forma que ela admita a maior quantidade possı́vel

de luz.

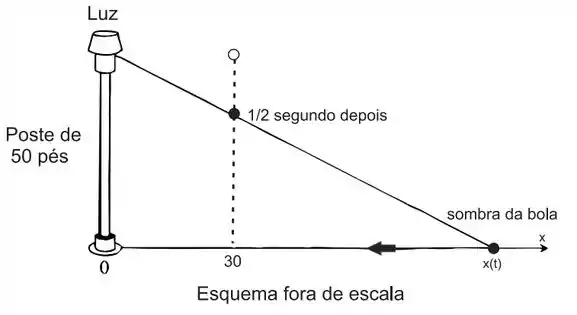
Uma luz está acesa no topo de um poste de 50 pés de altura. Uma bola cai da mesma altura em um ponto situado a 30 pés de distância do poste (Veja a figura a seguir). A que velocidade a sombra da bola se desloca no solo 1/2 segundo depois? (Considere que na queda a bola percorreu s = 16t 2 pés em t segundos)

Quando f (x) derivável quando x = a, a variação aproximada do valor de f, quando x varia de a para a + △x é dado pelo diferencial total avaliado no ponto x = a, ou seja,

(variação da linearização de f correspondente à variação dx = △x). Use diferenciais para aproximar os números e . Essas aproximações estão superestimadas ou subestimadas?

Uso o Teorema do Valor Intermediário junto com o Teorema de Rolle para provar que o polinômio , possui um único zero real (raiz da equação .

Mostrar que a função , , tem exatamente um zero real.

Mostre que a equação tem no máximo duas raízes reais.

Estude o exemplo 1 página 297 de [ST]. Em seguida, encontre os intervalos nos quais f (x) é crescente ou decrescente nos seguintes casos:

Estude o exemplo 1 página 297 de [ST]. Em seguida, encontre os intervalos nos quais f (x) é crescente ou decrescente nos seguintes casos:

b)

Estude o exemplo 1 página 297 de [ST]. Em seguida, encontre os intervalos nos quais f (x) é crescente ou decrescente nos seguintes casos:

b)

Um empresário verificou que quando vendia liquidificadores a reais cada um, os clientes compravam um total de x = 8000/p liquidificadores por mês. Sabendo que em meses o preço dos liquidificadores será de reais, calcule a taxa de variação da demanda mensal de liquidificadores com relação ao tempo, daqui a 16 meses.

Usando o Teorema do Valor Médio prove as desigualdades

Para quaisquer .