Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra da Cadeia

Ver Teoria
Exercício 317123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 1.5c

Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior

da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é

s   =   2   c o s   ( t )   +   3 s e n   ( t ) ,   t   ≥   0   ,

onde s é medido em centímetros e t , em segundos. (Consideramos o sentido positivo como sendo

para baixo.)

Faça o desenho dos gráficos da velocidade e posição,

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Calc 1!!! Queremos desenhar os gŕaficos da velocidade e posição do movimento descrito por:

s   =   2   c o s   ( t )   +   3 s e n   ( t ) ,   t   ≥   0   ,

Vamos nessa!

Passo 2

Começando com o gráfico da posição,

s   =   2   c o s   ( t )   +   3 s e n   ( t ) ,   t   ≥   0   ,

Aqui temos uma soma de funções periódicas com período 2 π , logo s também terá período 2 π . Temos que em t = 0

s   =   2  

E s atinge seu máximo quando

  - 2 s i n   ( t )   +   3 c o s   ( t ) = 0   ,

⇒ t = a r c t g ( 3 / 2 )

Logo, nossa curva fica da seguinte forma:

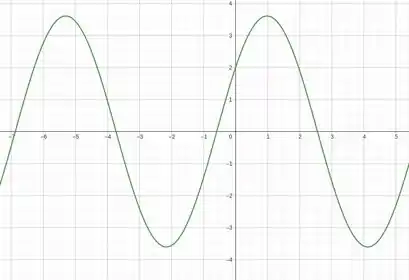
Passo 3

O gráfico da velocidade, Como

v = - 2 s i n ( t ) + 3 c o s ( t )

Aqui temos uma soma de funções periódicas com período 2 π , logo s também terá período 2 π . Temos que em t = 0

v =   3  

E s atinge seu máximo quando

  - 2 c o s ( t ) - 3 s i n   ( t ) = 0   ,

⇒ t = a r c t g ( - 2 / 3 )

t = - a r c t g ( 2 / 3 )

Logo, nossa curva fica da seguinte forma:

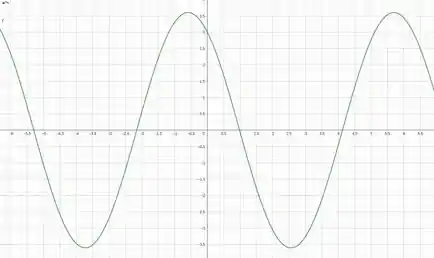
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento Acima

Exercícios de Livros Relacionados

Encontre a derivada da função.y = ((x^2 + 1)/(x^2 - 1))^3
Encontre a derivada da função.(d)/(d x) 2^(sen ( pi x ))
Encontre a derivada da função. y = r r 2 + 1
Encontre a derivada da função. G y = y - 1 4 y 2 + 2 y 5
Encontre a primeira e a segunda derivadas da função. y = e α x β x