UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 9.4
Um cartaz deve conter 50 de matéria impressa com duas margens de 4 cm cada, na parte superior e na parte inferior e duas margens laterais de 2 cm cada. Determine as dimensões externas do cartaz de modo que sua área total seja mínima.
Passo 1
Eaew, belezinha?
A questão nos pede para determinar as dimensões externas de um cartaz de modo que a sua área seja mínima. Vamos chamar as laterais da parte impressa do cartaz de a b, tal que temos a condição
Agora, vamos chamar as dimensões externas do cartaz de x e de y.
Sabemos que, o tamanho da dimensão y tem de ser b mais as duas margens verticais de 4 cm, . Semelhantemente, para x, com as duas margens horizontais de 2 cm, temos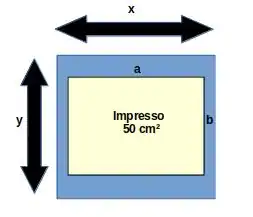 
Então, a área total do cartaz é .
Logo, temos que a área total A do cartaz é uma função de duas variáveis A = A(a,b). Mas, a gente sabe que a e b estão relacionados pelo vínculo da área impressa de 50 cm². Então, podemos substituir uma das variáveis, fazendo
Desse modo, temos que a área total é . Agora que temos a área total em função de um único parâmetro, podemos descobrir qual valor desse parâmetro minimiza a função igualando sua derivada a zero! Então vamos lá derivar a função!
Passo 2
Como a derivada de uma soma de funções é simplesmente a soma das derivadas, temos que a derivada da área é
Igualando isso a zero, obtemos que b deve ser:
Então, para que a área total do cartaz seja a menor possível, b deve ser igual à 10 cm e , consequentemente, a deve ser igual à 5 cm para que a área impressa seja igual à 50 cm². Como as dimensões externas são e , chegamos aos valores de x = 9cm e y = 18cm .
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
9 cm e 18 cm