Profº Sato - Listas de Cálculo 1 de Cálculo 1 da UFU - 1ª Lista de Exercícios

Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:

e .

Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:

Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:

e .

3. Se existir, faça um esboço da região do plano definida pelo sistema de desigualdades dados, nos seguintes casos:

(d) e .

1. Determine os zeros (caso existam) e o vértice das funções quadráticas seguintes. Em seguida, esboce seus gráficos:

(a)

1. Determine os zeros (caso existam) e o vértice das funções quadráticas seguintes. Em seguida, esboce seus gráficos:

(b)

Usando o conhecimento do gráfico de função , da identidade dado pelo produto notável e a noção de deslocamento horizontal, trace um esboço do gráfico das seguintes funções:

(a) .

Usando o conhecimento do gráfico de função , da identidade dado pelo produto notável e a noção de deslocamento horizontal, trace um esboço do gráfico das seguintes funções:

(b) .

Usando o conhecimento do gráfico de função , completamento de quadrados e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:

(a)

Usando o conhecimento do gráfico de função , completamento de quadrados e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:

(b)

6. Determine as raízes com suas respectivas multiplicidades das seguintes equações polinomiais:

(a) ;

6. Determine as raízes com suas respectivas multiplicidades das seguintes equações polinomiais:

(b) ;

7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico

(a) ;

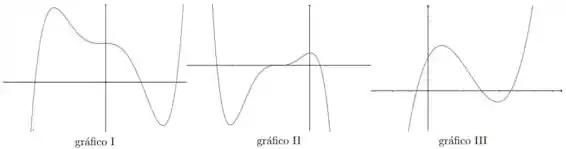
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico

(b) ;

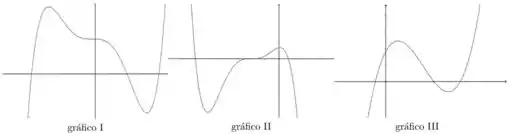
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico

(c) ;

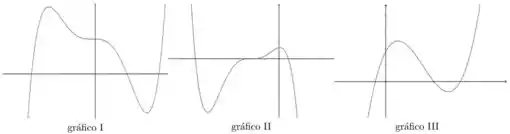
8. Determine o domínio e execute as operações indicada nas expressões abaixo. Em seguida, simplifique essas expressões, fatorando numerador e o denominador, caso necessário.

(a) .

8. Determine o domínio e execute as operações indicada nas expressões abaixo. Em seguida, simplifique essas expressões, fatorando numerador e o denominador, caso necessário.

(b) .

9. Usando o conhecimento do gráfico da função potência , para um inteiro , produtos notáveis e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:

(i) .

9. Usando o conhecimento do gráfico da função potência , para um inteiro , produtos notáveis e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:

(ii) .

1. Caso existam, defina as funções , , e nos casos dados a seguir. Em cada caso, determine o domínio da função resultante.

(a) ; .

1. Caso existam, defina as funções , , e nos casos dados a seguir. Em cada caso, determine o domínio da função resultante.

(b) ; .

Determine onde cada uma das seguintes funções é descontínua:

Determine onde cada uma das seguintes funções é descontínua:

Determine os pontos que

é contínua, e classifique suas descontinuidades.

Caso existam, defina as funções , , e nos casos dados a seguir. Em cada caso, determine o domínio da função resultante.

; .

Dada , encontre as funções , e tais que .

Se e , encontre uma função tal que (Pense sobre quais operações deveriam ser feitas em para chegar em ).

Se e , encontre uma função tal que .

Se e , encontre uma função tal que .

Determine os intervalos para os quais as funções seguintes são crescentes e decrescentes.

Determine os intervalos para os quais as funções seguintes são crescentes e decrescentes.

Use um recurso gráfico para determinar os intervalos de crescimento e decrescimento das funções:

;

Use um recurso gráfico para determinar os intervalos de crescimento e decrescimento das funções:

.

Admitindo as propriedades das funções potências, é possível resolver esse exercício sem o auxílio computacional?

Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:

Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:

Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:

Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:

Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:

Considere a função cujo gráfico é dado a seguir e faça o que se pede

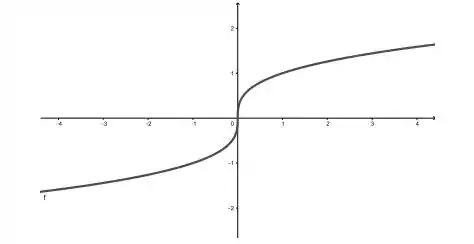
Justifique a afirmação é uma função injetora;

Considere a função cujo gráfico é dado a seguir e faça o que se pede

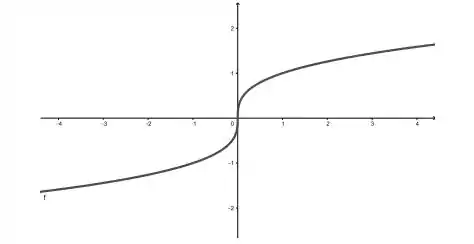
Determine o domínio e a imagem da função inversa de ;

Considere a função cujo gráfico é dado a seguir e faça o que se pede

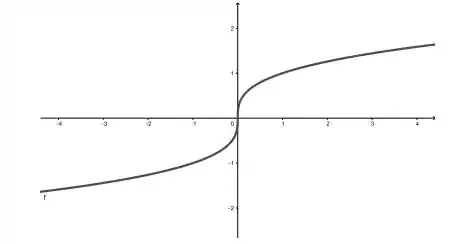
Estime o valor de .

Suponha que você receba uma oferta para trabalhar por apenas um mês. Qual das seguintes formas de pagamento você prefere?

Um milhão de dólares no fim do mês.

Um centavo de dólar no primeiro dia do mês, dois centavos no segundo dia, quatro centavos no terceiro dia, e em geral, centavos de dólar no n-ésimo dia.

Numa epidemia de gripe, o número de pessoas num bairro que pegaram gripe após dias é dado por:

Quantas pessoas foram infectadas após dia? Após dias?

Numa epidemia de gripe, o número de pessoas num bairro que pegaram gripe após dias é dado por:

Em quantos dias pessoas ficaram com gripe?

Encontre a função exponencial cujo gráfico é dado abaixo. Em seguida, determine o gráfico da sua inversa, bem como sua lei de formação.

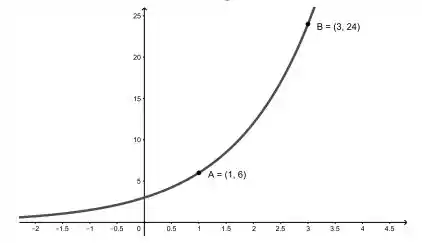
Sejam f uma função definida em R. Mostre que as funções

e

são funções, respectivamente, par e ímpar. Em seguida, mostre que toda função com domínio R pode ser escrita com soma de uma função par com uma função ímpar.

Se as funções

e

são denominadas cosseno hiperbólico e seno hiperbólico, respectivamente. Demostre as seguintes identidades trigonométricas hiperbólicas:

em que tagh e cosh são, respectivamente, as funções tangente e cossecante hiperbólicas.

Esboce os gráficos das funções abaixo. Qual é o período de cada uma?

Esboce os gráficos das funções abaixo. Qual é o período de cada uma?

(b)

Esboce os gráficos das funções abaixo. Qual é o período de cada uma?

(c)

Esboce os gráficos das funções abaixo. Qual é o período de cada uma?

(d)

Encontre a forma Fase-Amplitude em termos de uma senoide e, também, em termos de uma cossenóide, das seguintes funções:

(a) ;

Encontre a forma Fase-Amplitude em termos de uma senoide e, também, em termos de uma cossenóide, das seguintes funções:

(b) ;

Faça um esboço do gráfico de cada uma das inversas das seguintes funções trigonométricas (primeiro verifique qual é o domínio e imagem a dessas funções!): f (x) = cos (x), g (x) = sen (x ) e h (x) = tag (x )

Mostre que e que .

Definir uma função y = g(x) tal que , mas g não é definida em x=2.

Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.

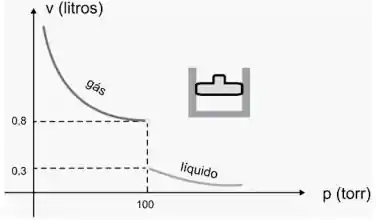
(a)

Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.

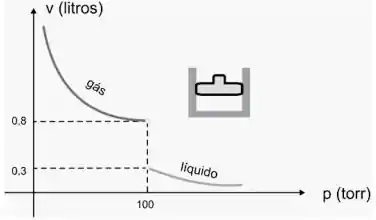
(b)

Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.

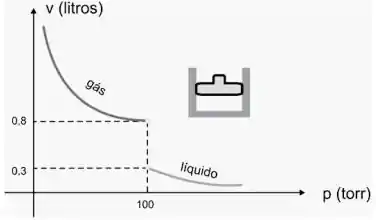
(c) Existe . Por que?

Encontre o valor do limite indicado a seguir. E, conforme o caso, indique os Teoremas de limite usados (Propriedades Operatórias de Limites).

(a)

Encontre o valor do limite indicado a seguir. E, conforme o caso, indique os Teoremas de limite usados (Propriedades Operatórias de Limites).

(b)

Encontre o valor do limite indicado a seguir. E, conforme o caso, indique os Teoremas de limite usados (Propriedades Operatórias de Limites).

(c)

6.4 Se existem, calcule os seguintes limites:

a)

6.4 Se existem, calcule os seguintes limites:

b)

6.4 Se existem, calcule os seguintes limites:

c)

6.4 Se existem, calcule os seguintes limites:

d)

6.4 Se existem, calcule os seguintes limites:

e)

6.4 Se existem, calcule os seguintes limites:

f)

6.5 Se , desenvolva a expressão obtendo igualdade . Em seguida, calcule o limite

6.6 Se , desenvolva a expressão obtendo a igualdade . Em seguida, calcule o limite

7.1 Na Teoria da relatividade, a massa de uma partícula com velocidade é

Em que é a massa da partícula em repouso e a velocidade da luz. O que acontece quando tende ao valor ?

7.2 Se existem, calcule os seguintes limites:

a)

7.2 Se existem, calcule os seguintes limites:

b)

7.2 Se existem, calcule os seguintes limites:

c)

7.2 Se existem, calcule os seguintes limites:

d)

7.2 Se existem, calcule os seguintes limites:

e)

7.2 Se existem, calcule os seguintes limites:

f)

7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.

a)

7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.

b)

7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.

c)

7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.

d)

7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.

e)

7.3 Para as funções abaixo, encontre os limites quando (i) e (ii) . Em seguida, determine quais funções admite uma assíntota horizontal. Inclua as equações e os gráficos das assíntotas, bem como um esboço dos gráficos dessas funções indicando o(s) comportamento(s) assintóticos no infinito.

f)

7.4. Estude as assíntotas horizontais da função

7.5 Explique por que a função é descontínua no ponto indicado, em seguida, esboce o gráfico da função, nos seguintes casos.

a) ponto .

7.5 Explique por que a função é descontínua no ponto indicado, em seguida, esboce o gráfico da função, nos seguintes casos.

b) ponto .

7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.

a)

7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.

b)

7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.

c)

7.7 Esboce o gráfico das seguintes funções:

a)

b)

c)

d)

7.7 Esboce o gráfico das seguintes funções:

a)

b)

c)

d)

7.7 Esboce o gráfico das seguintes funções:

a)

b)

c)

d)

7.7 Esboce o gráfico das seguintes funções:

a)

b)

c)

d)

8.1 Determine o valor da constante de modo que seja contínua a função dada por

8.2 Determine onde cada uma das funções é descontínua:

a)

Em seguida, classifique essas descontinuidades.

Para cada uma das funções seguintes determine o(s) valor(es) de para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).

Para cada uma das funções seguintes determine o(s) valor(es) de para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).

Para cada uma das funções seguintes determine o(s) valor(es) de para o(s) qual(quais) a função é descontínua. identifique o(s) tipo(s) de descontinuidade(s). Nos casos possíveis, encontra uma nova definição para a função de modo a remover qualquer (quaisquer) descontinuidade(s) removível (removíveis).

1. Durante uma epidemia de dengue, o número de pessoas que adoeceram, num certo bairro, após dias é dado por:

(a) Determine a quantidade máxima de indivíduos atingidos pela doença.

1. Durante uma epidemia de dengue, o número de pessoas que adoeceram, num certo bairro, após dias é dado por:

(b) Esboce o gráfico de

2. O número de pessoas infectadas por uma epidemia de dengue é modelado por:

(a) Esboce o gráfico de .

2. O número de pessoas infectadas por uma epidemia de dengue é modelado por:

(b) A epidemia de dengue passará a longo prazo? Justifique sua resposta

3. Para cada um dos itens abaixo:

(i) Prove que a equação tem pelo menos uma raiz real.

(ii) Use sua calculadora para encontrar o intervalo de comprimento que contenha uma raiz.

(a) .

3. Para cada um dos itens abaixo:

(i) Prove que a equação tem pelo menos uma raiz real.

(ii) Use sua calculadora para encontrar o intervalo de comprimento que contenha uma raiz.

(b) .

4. Verifique se as seguintes equações admitem, pelo menos, uma raiz real:

(a) ;

4. Verifique se as seguintes equações admitem, pelo menos, uma raiz real:

(b) ;

1. Use a continuidade para calcular o limite seguintes:

a)

b)

2. Encontre, quando existir, o limite. Em qualquer caso, explique sua conclusão.

a)

2. Encontre, quando existir, o limite. Em qualquer caso, explique sua conclusão.

b)

3. Use o Teorema do Confronto para mostrar que . Ilustre fazendo os gráficos, no mesmo sistema de coordenadas, , e .

4. Determine os seguintes limites

(a) e ;

4. Determine os seguintes limites

(b) e ;

4. Determine os seguintes limites

(c) ;

4. Determine os seguintes limites

(d) ;

Sugestão:

5. Usando um Corolário do Teorema do Confronto, mostre que a função tem limite no ponto nos seguintes casos:

(a) e

5. Usando um Corolário do Teorema do Confronto, mostre que a função tem limite no ponto nos seguintes casos:

(b) e

Sugestão: Obtenha uma fatoração do tipo , em que é limitada próximo do ponto e

6. Usando o limite fundamental dado pela igualdade calcule os seguintes limites: