UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 9.5
Encontre a área do maior retângulo que pode ser inscrito em um semi-cı́rculo de raio r.
Passo 1
Eaew, belezinha?
A questão nos pede para determinar a área do maior retângulo que pode ser inscrito em meio círculo. Vamos dar uma olhada na situação:
Bem, da imagem a gente vê que a área do retângulo vermelho é dada pela base vezes a altura: . Então, vemos que a área do retângulo é uma função de duas variáveis. No entanto, as medidas de x e y estão relacionadas através de um triângulo retângulo: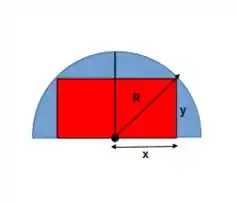
Então, podemos escrever a função da área como
Agora, para encontrar qual valor de x maximiza essa função, tudo que precisamos fazer é derivá-la e igualar isso à zero, porque a gente sabe que, nos pontos de extremo de uma função, a sua derivada é nula. Então vamos lá derivar!
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Passo 2
A função A(x) consiste de um produto de duas funções: e . Então, vamos utilizar a regra do produto para derivar. Sabendo que a derivada de f(x) é e que a derivada de g(x) é , vamos usar que a derivada de um produto de funções f(x)g(x) é para obter a derivada de A(x). Assim, temos
Para que a área seja máxima, essa expressão deve ser igual a zero. Então:
Então, o valor de x que maximiza a área do retângulo inscrito é . Agora, para descobrir a área máxima, só precisamos substituir o valor de x obtido na expressão para A(x). Vamos lá!
Passo 3
Como a área do retângulo é dada por , substituindo , obtemos a área máxima de
A questão foi isso! Te vejo na próxima! Tchau Tchau!