Exercícios Resolvidos de Taxa Relacionada

Ver Teoria

Exercício 131 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 4.1b

Se um tanque contém, inicialmente, 5.000 galões de água, que escoa pelo fundo em 40 minutos,

então a Lei de Torricelli dá o volume V de água que restou no tanque depois de t minutos como

,em que

Em que instante o fluxo é mais rápido? E mais vagaroso? Resuma o que você encontrou.

Passo 1

Eaew, belezinha?

O enunciado nos dá uma função que, para cada instante de tempo entre 0 minutos e 40 minutos, nos retorna o volume de água em galões que o tanque possui nesse instante de tempo. Por exemplo, para t = 0, ou seja, no instante inicial, temos que o galão se encontra completamente cheio, se substituirmos t = 0 na função , enquanto que, no instante final, em t = 40 minutos, temos que o tanque está completamente vazio, porque . A questão pede para determinar o instante de tempo em que o fluxo é mais rápido e mais vagaroso, então para isso, precisamos calcular sua derivada temporal para descobrir como a função varia no tempo! Bora derivar então! Para derivar essa função vamos utilizar a regra da cadeia, pois a função pode ser vista como uma composição das funções e . Assim, a função pode ser escrita como e sua derivada será dada através da regra da cadeia

Agora, temos uma função que para cada instante de tempo t dado nos dá a taxa de escoamento do tanque!

Passo 2

Agora que possuímos a função derivada, podemos analisá-la para determinar em quais instantes o fluxo é mais rápido ou mais vagaroso. Primeiro, note que a função derivada é uma reta decrescente, o que qualitativamente é intuitivo, visto que a quantidade de água no tanque diminui com o tempo. Sendo uma reta definida em um intervalo finito, temos que a função derivada terá um valor mínimo e máximo global. Nesse caso, no intervalo para o qual a função está definida, , temos que, em módulo, o maior valor que a função derivada assume ocorre quando t = 0 pois , quando ocorre o maior fluxo de água pelo tanque. Similarmente, temos que o momento em que o fluxo atinge seu valor mínimo, ocorre quando t = 40 minutos, quando a derivada atinge seu valor mínimo, em módulo, porque . A figura abaixo representa, em vermelho, o gráfico do volume de água no tanque em função do tempo e em verde a derivada do volume em relação ao tempo.

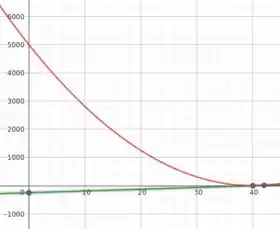
Resposta

Fluxo mais rápido: t = 0 min

Fluxo mais vagaroso: t = 40 min

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo

(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que

O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med

O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.

A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s