UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 9.3b
Uma empresa foi fundada em 1990 e sua capacidade de produção P = P (t) evoluiu segundo:
(b) Qual foi essa capacidade?
Passo 1
Eaew, belezinha?
O enunciado da questão nos pede para calcularmos o ano em que a empresa obteve a maior capacidade de produção, considerando o instante inicial t = 0 como o ano de fundação: 1990. Bem, para a gente obter os pontos de extremo de uma função, precisamos exigir que sua derivada seja nula. Mas por quê? Ora, em um ponto de máximo, a função não cresce a partir desse ponto, caso contrário ele não seria um máximo. E, em um ponto de mínimo, a função não diminui a partir desse outro ponto, se não ele não seria um ponto de mínimo. Imagina a seguinte situação: conforme você vai aumentando o valor de t, a função vai crescendo e crescendo até atingir seu valor máximo. A partir daí, ela tem que decrescer (para que esse ponto tenha sido máximo). Bem, a gente sabe que a derivada de uma função nos dá a taxa de variação dela em relação à variável do domínio. Então, para calcular os pontos de extremos, só precisamos exigir que a derivada seja nula, porque, para ser um ponto de extremo (ou de inflexão) de uma função contínua, a derivada tem que mudar de sinal! Se nos aproximamos de um ponto de máximo, a derivada deve ser positiva pois a função está crescendo para atingir seu máximo. Agora, após passar esse ponto, a derivada tem que ser negativa, porque a função tem que decrescer a partir do máximo, ou então ele não seria um máximo da função. Então, bora calcular a derivada? Vamos lá!
Passo 2
Para calcular a derivada da função P(t), vamos utilizar a regra da cadeia. Se definirmos as funções , e , temos que a função P(t) pode ser escrita como . Então, pela regra da cadeia, podemos derivar P(t) em relação a t, fazendo
Como , e , substituindo na expressão acima, obtemos
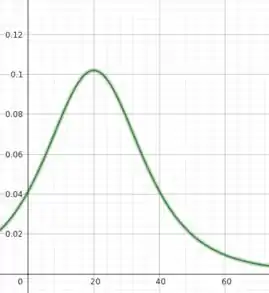
Como queremos que isso seja igual a zero, para que essa fração se anule, basta que o numerador se anule e o denominador seja não nulo. Assim, temos que . Portanto, temos que quando t =20, a derivada da função é nula, o que significa que a capacidade de produção atinge um extremo no ano de 1990 + 20 = 2010. Dá só uma olhada no gráfico:
Passo 3
Agora, para calcular qual foi a capacidade máxima de produção, só precisamos substituir o tempo em que isso ocorreu na função P(t) que nos dá a capacidade em função do tempo. Então vamo lá!
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
t = 20;
Ano: 2010;
Capacidade máx 0.102.