UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 5.2
Determinar a equação da reta tangente à curva , que seja paralela à reta . Esboçar os gráficos da função, da reta dada e da reta tangente encontrada. Determine, também, a reta normal à essa curva passando pelo ponto de tangência.
Passo 1
Eaew, belezinha?
A questão nos pede para determinar a equação de uma reta que tenha duas propriedades: i) ela tem que ser paralela à reta e ii) ela tem que ser tangente à curva em algum ponto. Primeiro, vamos dar uma olhada no gráfico dessas duas funções, beleza?
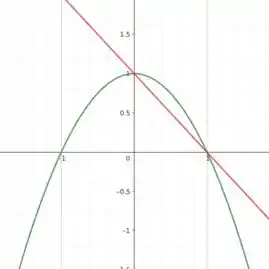
Bem, primeiro, a reta que procuramos tem que ser paralela à reta vermelha. Mas quando duas retas são paralelas? Quando elas têm o mesmo coeficiente angular! Então, como o coeficiente angular da reta é igual à -1, sabemos que a reta que procuramos possui coeficiente angular igual -1. Tá, mas e agora? Ora, agora precisamos descobrir qual é o valor de x que vai nos dar uma reta tangente à curva verde com esse coeficiente. Para isso, vamos calcular a derivada da função, já que ela nos dá o coeficiente da reta tangente à uma curva em cada ponto.
Passo 2
Então, bora derivar . Como a derivada da soma de funções é a soma da derivada dos termos individuais e, como 1 é uma constante, só precisamos derivar para obter uma função que vai nos dar a inclinação da reta tangente à curva y(x) em cada ponto. Fazendo isso, temos
Agora ficou fácil descobrir qual é o valor de x para o qual a reta tangente tem inclinação -1: é só igualar isso à expressão que encontramos para a derivada! Então, vamos fazer isso:
Ok, agora sabemos em que ponto x a reta tangente tem a mesma inclinação da reta dada. Mas, e agora? Falta mais alguma coisa, não? Bem, realmente, falta. Uma reta possui dois parâmetros: o coeficiente angular (que já foi determinado) e o coeficiente linear, que ainda não sabemos. O coeficiente linear não vai afetar em nada o paralelismo das duas retas, mas só existe uma reta com coeficiente angular -1 que irá ser tangente à curva no ponto com abscissa x = .
Descobrir o coeficiente linear é bem simples: como sabemos que a reta tangente tem que passar pelo ponto com abscissa e ordenada , basta substituir esses valores de coordenadas na equação da reta com o valor de a que obtivemos:
Então, o valor do coeficiente linear da reta procurada é . Com isso determinamos a equação da reta tangente procurada: , com vemos na reta azul da figura abaixo.
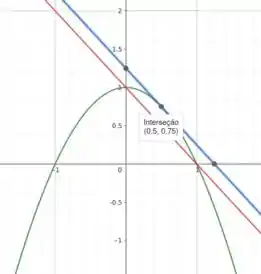
Passo 3
Agora só falta determinar a reta normal no ponto . E como a gente pode fazer isso? Como a derivada de uma função nos dá a inclinação da reta tangente, que é exatamente a tangente do ângulo que a reta faz com o eixo x, a gente sabe que um vetor que faça um ângulo de 135º graus com o eixo x tem a mesma direção da reta! Então, se pegarmos um vetor de componentes (-1,1), sabemos que ele tem a mesma direção da reta tangente porque o cateto oposto sobre o cateto adjacente é . Então, um segundo vetor com componentes (a,b) que tenha a mesma direção nossa reta normal tem que ser ortogonal ao vetor (-1,1) e deve passar pelo ponto (). Para que os vetores sejam ortogonais, precisamos que o produto escalar seja nulo: . Assim, para determinar um vetor, só precisamos que sua componente a seja igual à componente b. Então, a tangente da reta normal tem que ser . Logo, a inclinação da reta normal é igual à 1. Já determinamos a direção da reta, agora só precisamos que ela passe pelo ponto (). Então, vamos colocar essas coordenadas na equação da reta para determinar o coeficiente linear:
Então, . Logo, a equação da reta normal é . A reta normal está ilustrada na figura abaixo:
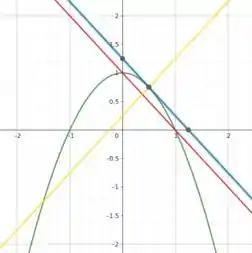
Resposta
Equação da reta tangente:
Equação da reta normal:
Resposta
Ei, a resposta está no passo a passo :)