UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 4.3
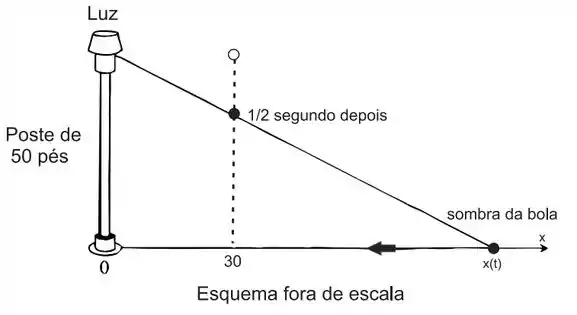
Uma luz está acesa no topo de um poste de 50 pés de altura. Uma bola cai da mesma altura em um ponto situado a 30 pés de distância do poste (Veja a figura a seguir). A que velocidade a sombra da bola se desloca no solo 1/2 segundo depois? (Considere que na queda a bola percorreu s = 16t 2 pés em t segundos)
Passo 1
Olá, aqui é Yuri e hoje iremos aplicar um pouco os conceitos de derivada para que possamos resolver essa questão. A velocidade nada mais é do que o quanto algo se desloca ao longo do tempo, sendo assim queremos saber
Da sombra da bola.
Se a altura da bola varia seguindo a equação
Passo 2
Podemos procurar saber a que altura a bola está em .
Com essa informação, poderemos utilizar conceitos de semelhança de triângulos para encontrar a altura da sombra nesse instante de tempo. Temos entao,
Logo temos
Com esse resultado em mão iremos montar um novo triangulo para que possamos calcular enfim a velocidade.
Passo 3
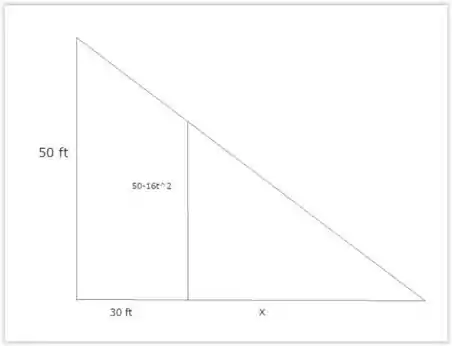
Com o novo triangulo, iremos fazer uma relação generalizada dos deslocamentos ao longo do tempo.
Agora iremos derivar em relação ao tempo,
Substituindo os valores previamente encontrados,