UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 4.2c
Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao
longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza
da força é
onde µ é uma constante chamada coeficiente de atrito. Se W = 50 lb e = 0, 6, faça um esboço do gráfico de F como uma função de e use-o para localizar o valor de para o qual .
Passo 1
Eaew, belezinha?
O enunciado da questão nos pede para calcular qual é a taxa de variação da força exercida em um objeto de peso W em relação ao ângulo . Vamos dar uma olhada na situação?
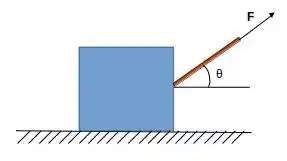
Então, a força sobre o objeto varia dependendo do ângulo que a corda faz com o objeto. Mas como podemos calcular essa taxa de variação? Calculando a derivada da força em relação ao ângulo!
Passo 2
Para calcular a derivada da força, vamos utilizar a regra da cadeia! A dependência da força com o ângulo pode ser escrita como
Olhando a expressão da força, reconhecemos que se trata de uma função composta. Se definirmos uma função e uma função , podemos escrever a força como
Como a derivada da soma de funções é simplesmente a soma das derivadas e, como as derivadas de seno e cosseno são, respectivamente, e , então
Passo 3
Finalmente, para descobrir quando a taxa de variação da força em relação ao ângulo é nula, precisamos igualar a derivada da força em relação à à zero. Fazendo isso, obtemos
Como , essa razão só será nula quando o numerador se anular. Portanto, queremos descobrir o valor do ângulo para o qual . Assim temos a relação para e :
Portanto, o ângulo para o qual a taxa de variação é nula é
Passo 4
Substituindo os parâmetros e W com os valores numéricos de 0.6 e 50 lb, respectivamente, temos que o ângulo para o qual a taxa de variação da força é nula é . Com o valor numérico de 0.6, temos que esse ângulo é de aproximadamente 0.54 rad. A figura a seguir ilustra o gráfico da força em função do ângulo.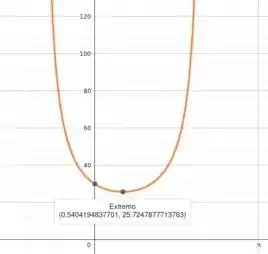
Resposta
Ei, a resposta está no passo a passo :)