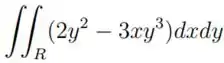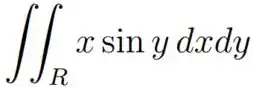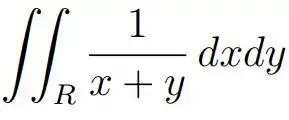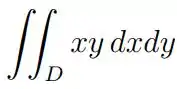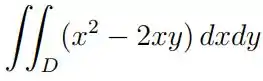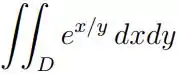Lista de Exercícios - USP de Cálculo 3 da USP - Lista 1 - 2022.1

Calcule as seguintes integrais duplas:

a)

Onde

Calcule as seguintes integrais duplas:

b)

Onde

Calcule as seguintes integrais duplas:

c)

Onde

Calcule as integrais iteradas

E

As respostas contradizem o Teorema de Fubini?

Calcule as seguintes integrais duplas:

a)

Onde

Calcule as seguintes integrais duplas:

b)

Onde

Calcule as seguintes integrais duplas:

c)

Onde

Determine o volume do sólido limitado pela superfície e os planos , ,

Determine o volume do s ́olido contido no primeiro octante limitado por e pelo plano

.

Uma piscina tem formato circular de raio e profundidade variando linearmente de sul a norte,

sendo que no extremo sul é de e no extremo norte é de . Calcule o volume da piscina.

, onde é a região limitada por

, onde é a região limitada por

, onde é a região do primeiro quadrante limitada pela circunferência de centro

e raio .

, onde é

, onde é

Determine o volume do sólido em cada um dos seguintes casos:

a) é limitado superiormente pelo paraboloide , inferiormente pelo plano e sua projeção no plano é a região limitada por e .

Determine o volume do sólido em cada um dos seguintes casos:

b) é limitado superiormente pelo paraboloide , inferiormente pelo plano e sua projeção no plano é o triângulo de vértices , e .

Determine o volume do sólido em cada um dos seguintes casos:

c) é a região do primeiro octante limitada pelo cilindro e pelo plano .

Determine o volume do sólido em cada um dos seguintes casos:

d) é limitado pelos planos , , e .

Determine o volume do sólido em cada um dos seguintes casos:

e) é a região do primeiro octante limitada pelo cilindro e pelos planos , e .

Determine o volume do sólido em cada um dos seguintes casos:

f) é limitado pelos cilindros e , onde .

Escreva duas integrais iteradas correspondentes à integral dupla , onde é a região do plano limitada pelas curvas e .

Calcule as seguintes integrais, invertendo a ordem de integração:

a)

Calcule as seguintes integrais, invertendo a ordem de integração:

b)

Calcule as seguintes integrais, invertendo a ordem de integração:

c)

Calcule as seguintes integrais, invertendo a ordem de integração:

d)

Calcule as seguintes integrais, invertendo a ordem de integração:

e)

Calcule as integrais:

a) , onde é o disco de centro na origem e raio .

Calcule as integrais:

b) , onde é a região do primeiro quadrante limitada pelas circunferências e .

Calcule as integrais:

c) , onde é a região interior à cardioide e exterior à circunferência .

Calcule as integrais:

d) , onde é a região limitada pelas espiras e , com .

Calcule as integrais:

e) , onde é a região limitada pelo semicírculo e o eixo .

Esboce a curva e calcule a área da região indicada:

a) a região limitada por um laço de rosácea

Esboce a curva e calcule a área da região indicada:

b) a região limitada pela lemniscata

Determine o volume da região interior à esfera e exterior ao cilindro , com .

Determine a massa e o centro de massa da lâmina que ocupa a região e tem densidade , nos seguintes casos:

a) e

Determine a massa e o centro de massa da lâmina que ocupa a região e tem densidade , nos seguintes casos:

b) é o triângulo de vértices , , e

Determine a massa e o centro de massa da lâmina que ocupa a região e tem densidade , nos seguintes casos:

c) é a região do primeiro quadrante limitada pela parábola e a reta e .

Determine a massa e o centro de massa da lâmina que ocupa a região e tem densidade , nos seguintes casos:

d) é a região limitada pela parábola e a reta e .

Determine a massa e o centro de massa da lâmina que ocupa a região e tem densidade , nos seguintes casos:

e) e .

Determine os momentos de inércia , e das lâminas descritas nos itens c) e d) do exercício anterior.

Calcule usando mudança de coordenadas:

a) , onde é o paralelogramo de vértice , , e .

Calcule usando mudança de coordenadas:

b) , onde é a região do primeiro quadrante limitada pelas retas e .

Calcule as integrais iteradas:

a)

Calcule as integrais iteradas:

b)

Calcule

, onde

Calcule

, onde onde D é a região abaixo do plano e acima da região no plano limitada pelas curvas

Calcule

, onde é o tetraedro sólido com vértices

Calcule

, onde é limitada pelos planos

Calcule

, onde é limitada pelo parabolóide

e pelo plano .

Determine a massa e o centro de massa do cubo cuja densidade é dada pela função

.

Determine os momentos de inércia de um cubo de densidade constante e aresta se um dos seus

vértices é a origem e três de suas arestas estão sobre os eixos coordenados.

.

Calcule a integral

onde é a região limitada pelo cilindro

Calcule a integral

onde é a região entre os cilindros e limitada pelos planos e por

Calcule as seguintes integrais:

c) , onde é o sólido limitado pelo cilindro , pelo cone e contido no semiespaço .

Determine o volume da região limitada pelos paraboloides e .

Determine a massa e o centro de massa do sólido limitado pelo paraboloide e pelo plano , se tem densidade constante .

Calcule as integrais:

(a) , onde é a bola unitária .

Calcule as integrais:

(b) , onde é a parte da bola unitária contida no primeiro octante.

Calcule as integrais:

(c) , onde é a região interior ao cone e à esfera .

Determine a massa de um hemisfério sólido de raio se a densidade em qualquer ponto é proporcional a sua distância ao centro da base.

Calcule o volume da região limitada pelo elipsoide .

Calcule , onde .

1. Calcule a massa de , com função densidade .

Calcule a massa de com função de densidade

Calcule o momento de Inercia com relação a origem de , onde e a função densidade

Calcule a massa do solido , com e .

Calcule o volume da região acima do cone e dentro da esfera .

Calcule a massa da região acima do cone dentro da esfera com .

Calcule a massa da região R limitada por:

1. , , com e e

Calcule a massa da região R limitada por:

com .

Calcule a massa da região R limitada por:

c) , com

Calcule a massa da região R limitada por:

d) , para com .

Calcule a massa da região R limitada por:

e) , com ;

Calcule a massa da região R limitada por:

, , para com .

1. Calcule para R limitada por: , , , , e ;

Calcule a massa do solido onde a densidade é .

Calcule onde R é limitada por:

1. , , para

Calcule onde R é limitada por:

b)

Calcule a integral

Use a transformação para calcular o volume da região limitada pela superfície e pelos planos coordenados.

Calcule a massa da região limitada por:

Com

Se D é a região limitada pelas curvas e e se

Então podemos afirmar que

O volume da região limitada pelo cone e pelo cilindro com , pode ser calculado usando coordenadas cilíndricas por

O volume do sólido limitado por e é

Calcule onde V é o solido limitado por

Calcule a massa do sólido limitado por , com sendo a densidade

O volume do sólido limitado pelo cilindro e pelo paraboloide é dado pelo valor da integral dupla:

Para o cálculo dessa integral, uma mudança de coordenadas conveniente e o respectivo Jacobiano (J) são