USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 39
O volume da região limitada pelo cone e pelo cilindro com , pode ser calculado usando coordenadas cilíndricas por
Passo 1
Beleza meu amigo? Aqui a gente não vai precisar resolver uma integral, iremos apenas analisar a sua estrutura, passar para coordenadas cilíndricas e depois encontrar os limites de integração. As coordenadas cilíndricas são
Passo 2
Vamos substituir no cilindro e ver o que encontramos
Tomando a vista superior de nossa região
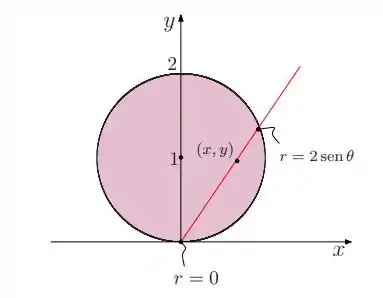
Notamos que o ângulo
Resposta
b)
Exercícios de Livros Relacionados
58. A base de S é a região delimitada pela parábola y = 1 - x 2 e pelo eixo x . As secções transversais perpendiculares ao eixo y são quadradas.
Considere S o sólido obtido pela rotação da região mostrada na figura em torno do eixo y . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume
Use os resultados desta seção para deduzir o Princípio de Cavalieri (Exercício 64 ).
Conforme a figura abaixo, a cúpula de uma catedral foi projetada com três suportes semicirculares de raio r , de modo que cada seção transversal horizontal é um hexágono regular. Mostre que o volume d